题目内容
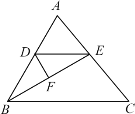
【题目】如图,![]() 是
是![]() 的两条高线,且它们相交于
的两条高线,且它们相交于![]() 是
是![]() 边的中点,连结
边的中点,连结![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,已知
,已知![]() .
.
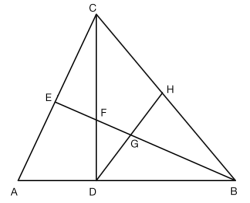
(1)求证BF=AC.
(2)若BE平分![]() .
.
①求证:DF=DG.
②若AC=8,求BG的长.
【答案】(1)证明见解析;(2)①证明见解析;②BG=![]() .
.
【解析】
(1)易证![]() 是等腰直角三角形,然后得到
是等腰直角三角形,然后得到![]() ,然后利用ASA证明Rt△DFB≌Rt△DAC,即可得到结论;
,然后利用ASA证明Rt△DFB≌Rt△DAC,即可得到结论;
(2)①由![]() 是等腰直角三角形,得到∠DCB=∠HDB=∠CDH=45°,由BE是角平分线,则∠ABE=22.5°,然后得到∠DFB=∠DGF,即可得到DF=DG;
是等腰直角三角形,得到∠DCB=∠HDB=∠CDH=45°,由BE是角平分线,则∠ABE=22.5°,然后得到∠DFB=∠DGF,即可得到DF=DG;
③连接CG,则BG=CG,然后得到△CEG是等腰直角三角形,然后有△AEB≌△CEB,则有CE=AE,即可求出BG的长度.
解:(1)证明:![]() ,BD=CD,
,BD=CD,
![]() 是等腰直角三角形.
是等腰直角三角形.
![]() ,
,![]() ,且
,且![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
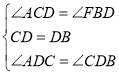 ,
,
Rt△DFB≌Rt△DAC(ASA),
![]() .
.
(2)①∵△BCD是等腰直角三角形
H点是CB的中点
∴DH=HB=CH
所以∠DCB=∠HDB=∠CDH=45°
∵BE平分∠ABC
∴∠ABE=22.5°
∴∠DFB=67.5°
∴∠DGF=∠DBF+∠HDB= 67.5°
∴∠DFB=∠DGF
∴DF=DG
②连接CG
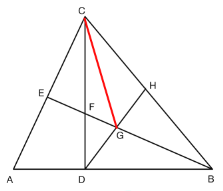
∵DH是中垂线
∴BG=CG
∴∠GCH=∠GBH=22.5°
∵Rt△DFB≌Rt△DAC
∴∠ACD=∠ABE=22.5°
∵∠DCB=45°
∴∠DCG=22.5°
∴∠ECG=45°
∵BE⊥AC
∴∠CEB=90°
∴△CEG是等腰直角三角形
在△AEB和△CEB中
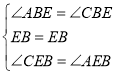
∴△AEB≌△CEB
∴CE=AE
∵AC=8
∴CE=AE=EG=4
∴CG=GB=![]() .
.

练习册系列答案
相关题目