题目内容
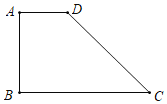
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是( )
A. 4<OC≤![]() B. 4≤OC≤
B. 4≤OC≤![]() C. 4<OC
C. 4<OC![]() D. 4≤OC
D. 4≤OC![]()
【答案】B
【解析】
作DE⊥BC于E,当⊙O与边AD相切时,圆心O与E重合,即OC=4;当OA=OC时,⊙O与AD交于点A,设OA=OC=x,则OB=6﹣x,在Rt△ABO中,由勾股定理得出方程,解方程得出OC=![]() ;即可得出结论.
;即可得出结论.
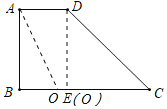
作DE⊥BC于E,如图所示:
则DE=AB=4,BE=AD=2,
∴CE=4=DE,
当⊙O与边AD相切时,切点为D,圆心O与E重合,即OC=4;
当OA=OC时,⊙O与AD交于点A,
设OA=OC=x,则OB=6﹣x,
在Rt△ABO中,由勾股定理得:42+(6﹣x)2=x2,
解得:x=![]() ;
;
∴以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是4≤x≤![]() ;
;
故选:B.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目