题目内容
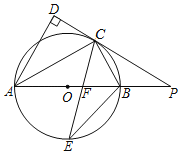
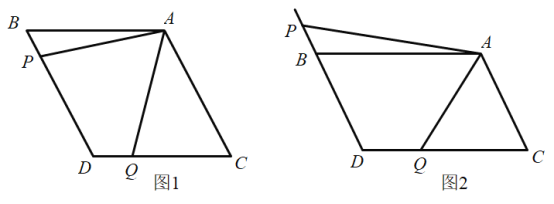
【题目】如图1,![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,且满足
上的点,且满足![]() .
.
(1)求证:![]()
(2)在图1中,是否存在与AP相等的线段?若存在,请找出来,并加以证明;若不存在,说明理由.
(3)若将“![]() 为
为![]() 上的点”改为:“
上的点”改为:“![]() 为DB延长线上的点”其他条件不变(如图2)若
为DB延长线上的点”其他条件不变(如图2)若![]() ,求线段
,求线段![]() 之间的数量关系(用含
之间的数量关系(用含![]() 的式子表示)
的式子表示)
【答案】(1)证明详见解析;(2)存在,![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)由已知可得四边形ABCD是菱形,结合菱形的性质,由![]() 可得
可得![]() ,即可求得
,即可求得![]() ;
;
(2)过点A作![]() ,交BD于点M,证得
,交BD于点M,证得![]() ,得
,得![]() ,即可得AP=AQ;
,即可得AP=AQ;
(3)过点A作![]() ,交BD的延长线于点M,作
,交BD的延长线于点M,作![]() ,可证
,可证![]() ,得
,得![]() ,即
,即![]() ,易证
,易证![]() ,即可得到
,即可得到![]() .
.
(1)证明:∵四边形ABCD是平行四边形,![]() ,
,
∴四边形ABCD是菱形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)存在,![]() .
.
如图,过点A作![]() ,交BD于点M,
,交BD于点M,
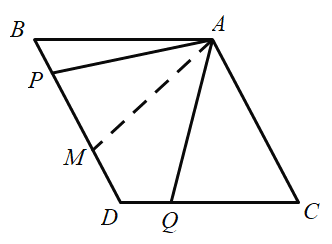
∴∠APM=∠AMP,
由(1)知,![]() ,
,
∴∠APM=∠AQC,
∴∠AMP=∠AQC,
又∵四边形ABCD为菱形,
∴AB=AC,∠B=∠C,
∴![]() ,
,
∴![]() ,
,
即AP=AQ.
(3)过点A作![]() ,交BD的延长线于点M,作
,交BD的延长线于点M,作![]() ,
,

∵四边形ABCD是平行四边形,
∴AC∥BD,∠C+∠BDC=180°,∠ACD=∠ABM,
∵![]() ,
,
∴∠PAQ+∠BDC=180°,
∴∠APB+∠AQD=180°,
∴∠APB=∠AQC,
又∵AP=AM,
∴∠APB=∠AMP,
∴∠AQC=∠AMP,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
在等腰△APM中,AH⊥PM,
∴![]() ,
,
![]() ,
,
即![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
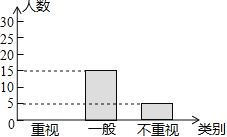
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.