题目内容
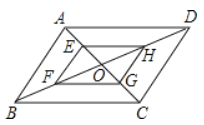
【题目】如图,△ABC是⊙O的内接三角形,直径AB垂直于弦CG,垂足为点H,过点C作ED⊥CG,交⊙O于点E,且∠CBD=∠A,连接BE,交CG于点F.
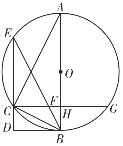
(1)求证:BD是⊙O的切线;
(2)求证:BC2=BF·BE;
(3)若CG=8,AB=10,求sin E的值.
【答案】(1)见解析;(2)见解析;(3)sin E=![]() .
.
【解析】
(1)利用直径所对的圆周角是直角,易证得∠ABD=90°,从而证得结论;
(2)利用垂径定理结合圆周角定理证得∠BCG=∠E,得到△CBF∽△EBC,利用对应边成比例,即可证明结论;
(3)连接OC,利用垂径定理求得CH =4,在Rt△OCH中,由勾股定理求得OH的长,在Rt△BCH中,由勾股定理求得BC的长,由于∠E=∠BCG,利用正弦函数即可求解.
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠CBA=90°.
∵∠CBD=∠A,
∴∠CBA+∠CBD=90°,即∠ABD=90°,
∴AB⊥BD,
∵OB是⊙O的半径,
∴BD是⊙O的切线;
(2)证明:∵AB⊥CG,
∴![]() =
=![]() ,
,
∴∠BCG=∠E,
又∠CBF=∠EBC,
∴△CBF∽△EBC,
∴![]() ,
,
∴BC2=BF·BE;
(3)连接OC.
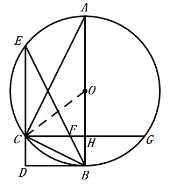
∵AB=10,CG=8,AB⊥CG,
∴CH=![]() CG=4,OB=OC=
CG=4,OB=OC=![]() AB=5,
AB=5,
在Rt△OCH中,由勾股定理,得OH=![]() ,
,
∴BH=OB-OH=2,
在Rt△BCH中,由勾股定理,得BC=![]() ,
,
由(2)得∠E=∠BCG,
∴sin E=sin∠BCG=![]() .
.

 阅读快车系列答案
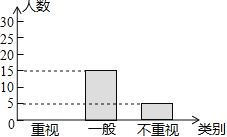
阅读快车系列答案【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.
【题目】为培养学生庭好的学习习惯,某校九年级年级组举行“整理错题集“的征集展示活动,并随机对部分学生三年“整理题集”中收集的错题数x进行了抽样调查,根据收集的数据绘制了下面不完整的统计图表.
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
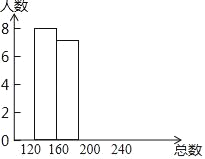
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
请你根据图表中的信息完成下列问题:
(1)频数分布表中a= ,b= ,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计整理的错题数在160或160题以上的学生有多少人?
(3)已知第一组中有两个是甲班学生,第四组中有一个是甲班学生,老师随机从这两个组中各选一名学生谈整理错题的体会,则所选两人正好都是甲班学生的概率是多少?