题目内容
【题目】如图,∠AOB=40°,点P在∠AOB的内部,点C,D分别是点P关于直线OA,OB的对称点,连接CD分别交OA,OB于点E、F.则∠EPF=___________.

【答案】100°
【解析】
根据线段垂直平分线的性质可得CE=PE,PF=FD,进而推出角的关系∠PEF=2∠C,∠PFE=2∠D,结合已知条件利用四边形的内角和得出∠AOB+∠MPN=180°,在△PEF中可得∠EPF+2∠C+2∠D=180°,即可得出答案.
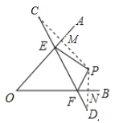
∵点C,D分别是点P关于直线OA,OB的对称点
∴CE=PE,PF=FD
∴∠PEF=2∠C,∠PFE=2∠D
∠PME=∠PNF=90°
在四边形OMPN中
∴∠AOB+∠MPN=180°
∵∠EPF+2∠C+2∠D=180°
∴∠MPN+∠C+∠D=180°
∴∠C+∠D=∠AOB=40°
∴∠EPF=100°
故答案为:100°.

练习册系列答案
相关题目