��Ŀ����
����Ŀ����ѧ��С������ٴ�ҵ������һ�ֽ���Ϊ![]() Ԫ/��������ܣ����۹����з��֣�ÿ���������٣����������۵���
Ԫ/��������ܣ����۹����з��֣�ÿ���������٣����������۵���![]() ��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����
��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����![]()
![]() ���С����Ҫÿ�ܻ��
���С����Ҫÿ�ܻ��![]() Ԫ��������ô���۵���Ӧ��Ϊ����Ԫ��
Ԫ��������ô���۵���Ӧ��Ϊ����Ԫ��
![]() ��С��ÿ�ܻ������Ϊ
��С��ÿ�ܻ������Ϊ![]() ��Ԫ���������۵��۶�Ϊ����Ԫʱ��ÿ�ܿɻ�����������������Ƕ��٣�
��Ԫ���������۵��۶�Ϊ����Ԫʱ��ÿ�ܿɻ�����������������Ƕ��٣�
![]() ��������ܵ����۵��۲��ø���
��������ܵ����۵��۲��ø���![]() Ԫ�����С����Ҫÿ�ܻ�õ�������
Ԫ�����С����Ҫÿ�ܻ�õ�������![]() Ԫ����ô�������۵���Ӧ��Ϊ���٣�
Ԫ����ô�������۵���Ӧ��Ϊ���٣�
���𰸡�(1)���۵���Ӧ��Ϊ![]() Ԫ��
Ԫ��![]() Ԫ��(2) ���ۼ�Ϊ
Ԫ��(2) ���ۼ�Ϊ![]() Ԫ/̨ʱ���������Ϊ
Ԫ/̨ʱ���������Ϊ![]() Ԫ��(3) �������۵���Ӧ��Ϊ
Ԫ��(3) �������۵���Ӧ��Ϊ![]() Ԫ��
Ԫ��![]() Ԫ֮�䣮
Ԫ֮�䣮
��������
��1��������=������ÿ���������赥�۶�ΪxԪ��w=����2x+100����x��20��=��2x2+140x��2000����w=400�����x���ɣ���2����w�Ľ���ʽ��Ϊ����ʽ��⼴�ɣ���3������������ͼ����ͼ��д��x�ķ�Χ����.
(1) w=����2x+100����x��20��=��2x2+140x��2000��
��w=400����2x2+140x��2000=400��
���x1=30��x2=40��
���۵���Ӧ��Ϊ30Ԫ��40Ԫ��
(2)w=(x��20)(��2x+100)=��2x2+140x��2000=��2(x��35)2+450��
�൱x=35ʱ��wȡ�����ֵ�����ֵΪ450Ԫ��
(3)����w��ͼ��
��y=0��2x2+140x��2000=0��
���x1=20��x2=50��
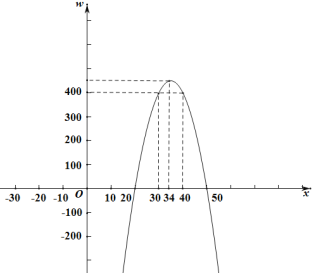
��ͼ���ѵó���30��x��34��
�������۵���Ӧ����30Ԫ��34Ԫ֮��.