Question

【题目】定理：直角三角形斜边上的中线等于斜边的一半．

（1）写出这个定理的逆命题；

（2）判断逆命题的真假并说明你的理由．

Answer 1

【答案】（1）三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形；（2）真命题，理由见解析

【解析】

（1）写出逆命题即可；

（2）根据直角三角形的判定解答即可．

解：（1）直角三角形斜边上的中线等于斜边的一半的逆命题为：三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．

（2）真命题.证明如下：

已知：如图，在△ABC中，点D是AB的中点，连接CD，且CD＝AB．

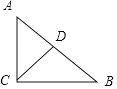
求证：△ABC是直角三角形．

证明：∵点D是AB的中点∴AD＝BD

∵CD＝AB，

∴AD＝BD＝CD，

∴∠DAC＝∠ACD，∠DCB＝∠DBC

∵∠DAC+∠ACD+∠DCB+∠DBC＝180°

∴∠ACD+∠DCB＝90°，即∠ACB＝90°

∴△ABC是直角三角形．