题目内容
【题目】如图,一圆弧形桥拱的圆心为![]() ,拱桥的水面跨度
,拱桥的水面跨度![]() 米,桥拱到水面的最大高度
米,桥拱到水面的最大高度![]() 为
为![]() 米.求:
米.求:

![]() 桥拱的半径;
桥拱的半径;
![]() 现水面上涨后水面跨度为
现水面上涨后水面跨度为![]() 米,求水面上涨的高度为________米.
米,求水面上涨的高度为________米.
【答案】(1)50;(2)10.
【解析】
(1)根据垂径定理和勾股定理求解;
(2)由垂径定理求出MH,由勾股定理求出EH,得出HF即可.
(1)如图,
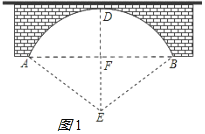
设点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
则由垂径定理知,点F是AB的中点,AF=FB=![]() AB=40,EF=ED-FD=AE-DF,
AB=40,EF=ED-FD=AE-DF,
由勾股定理知,AE2=AF2+EF2=AF2+(AE-DF)2,
设圆的半径是r,
则:r2=402+(r-20)2,
解得:r=50;
即桥拱的半径为50米;
(2)设水面上涨后水面跨度MN为60米,MN交ED于H,连接EM,如图2所示
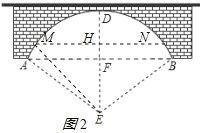
则MH=NH=![]() MN=30,
MN=30,
∴EH=![]() =40(米),
=40(米),
∵EF=50-20=30(米),
∴HF=EH-EF=10(米);
故答案为:10.

练习册系列答案
相关题目