题目内容
【题目】如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是 . 
【答案】相交
【解析】解:如图连接PC交MN于D,取MN的中点O,连接OP,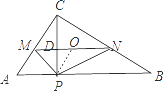
由题意PD<OP,
∴圆心O到直线AB的距离小于⊙O的半径,
∴以MN为直径的圆与直线AB相交,
故答案为相交;
设圆心O到直线l的距离为d,⊙O的半径为r,如果d ![]() r,那么直线与圆相交。如图连接PC交MN于D,取MN的中点O,连接OP,由题意可知PD<OP,即圆心O到直线AB的距离小于⊙O的半径,所以以MN为直径的圆与直线AB的位置关系是相交。
r,那么直线与圆相交。如图连接PC交MN于D,取MN的中点O,连接OP,由题意可知PD<OP,即圆心O到直线AB的距离小于⊙O的半径,所以以MN为直径的圆与直线AB的位置关系是相交。

练习册系列答案
相关题目
【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表![]() 单位:环
单位:环![]() :
:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
甲 | 10 | 9 | 8 | 8 | 10 | 9 |
乙 | 10 | 10 | 8 | 10 | 7 | 9 |
根据表格中的数据,可计算出甲、乙两人的平均成绩都是9环.
(1)分别计算甲、乙六次测试成绩的方差;
(2)根据数据分析的知识,你认为选______名队员参赛.


