Question

【题目】在平面直角坐标系中，已知A（﹣1，5），B（4，2），C（﹣1，0）三点．点A关于原点O的对称点A′，点B关于轴的对称点为B′，点C关于轴的对称点为C′.

（1）A′的坐标为　 　，B′的坐标为　 　，C′的坐标为　 .

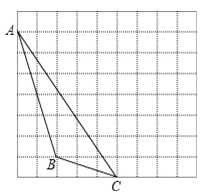
（2）建立平面直角坐标系，描出以下三点A、B′、C′，并求△AB′C′的面积．

Answer 1

【答案】（1）（1，-5），（4，-2）、（1，0）；（2）图详见解析，7.5 .

【解析】

（1）关于原点对称的两点的横、纵坐标都是互为相反数；关于x轴对称的两点的横坐标相同，纵坐标互为相反数；关于y轴对称的两点的横坐标互为相反数，纵坐标相同；

（2）根据点A′（1，-5），B′（4，-2），C′（1，0）在平面直角坐标系中的位置，可以求得A′C′=5，B′D=3，所以由三角形的面积公式进行解答．

解：（1）∵A（-1，5），

∴点A关于原点O的对称点A′的坐标为（1，-5）．

∵B（4，2），

∴点B关于x轴的对称点B′的坐标为（4，-2）．

∵C（-1，0），

∴点C关于y轴的对称点C′的坐标为（1，0）．

故答案为：（1，-5），（4，-2），（1，0）．

（2）如图，

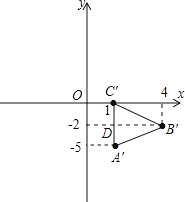
∵A′（1，-5），B′（4，-2），C′（1，0）．

∴A′C′=|-5-0|=5，B′D=|4-1|=3，

，即△A′B′C′的面积是7.5．