题目内容
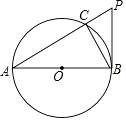
【题目】如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD. 
(1)求证:△ACD∽△BAD;
(2)求证:AD是⊙O的切线.
【答案】
(1)证明:∵AB=AD,
∴∠B=∠D,
∵AC=CD,
∴∠CAD=∠D,
∴∠CAD=∠B,
∵∠D=∠D,
∴△ACD∽△BAD
(2)证明:连接OA,
∵OA=OB,
∴∠B=∠OAB,
∴∠OAB=∠CAD,
∵BC是⊙O的直径,
∴∠BAC=90°,
∴OA⊥AD,
∴AD是⊙O的切线.

【解析】(1)根据等腰三角形的性质得到∠CAD=∠B,由于∠D=∠D,于是得到△ACD∽△BAD;(2)连接OA,根据的一句熟悉的性质得到∠B=∠OAB,得到∠OAB=∠CAD,由BC是⊙O的直径,得到∠BAC=90°即可得到结论.
【考点精析】认真审题,首先需要了解切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目