Question

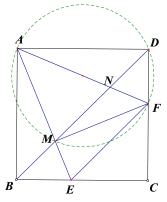
【题目】在正方形ABCD中，E、F分别为BC、CD边上的两个动点，∠EAF＝45°，下列几个结论中：①EF＝BE＋DF；②MN2＝BM2＋DN2；③FA平分∠DFE；④连接MF，则△AMF为等腰直角三角形；⑤∠AMN＝∠AFE． 其中一定成立的结论有（ ）

A.2个B.3个C.4个D.5个

Answer 1

【答案】D

【解析】

通过图形的旋转，得到，证明，可得①正确；将绕点A逆时针旋转得到，连接NG，证得，可得②正确；根据可得③正确；由∠BDC=∠MAN=45°，可得点A，M，F，D四点共圆，进而可得到④正确；通过证明三角形相似可得⑤正确；

∵四边形ABCD正方形，

∴AB=AD，，

∴将绕点A逆时针旋转得到，如图所示，

则AH=AE，，

∴，

∴，

∵AF=AF，

∴，

∴EF=FH=DF+DH=DF+BE，故①正确；

如图所示，

将绕点A逆时针旋转得到，连接NG，易证，是直角三角形，

∴MN=GN，

∴,故②正确；

由①可得，，

∴，

∴FA平分∠DFE，故③正确；

∵BD是正方形ABCD的对角线，

∴∠BDC=45°，

∵∠MAN=45°，

∴∠BDC=∠MAN，

∴点A，M，F，D四点共圆，

∵∠ADF=90°，

∴∠AMF=90°，

∴则△AMF为等腰直角三角形，故④正确；

由∠MAN＝∠FDN=45°，，可得到，

∴,

又∵，

∴∠AMN＝∠AFE，故⑤正确；

故答案选D．