ÌâÄ¿ÄÚÈİ
¡¾ÌâÄ¿¡¿Ä³Æ·ÅÆ·ş×°¹«Ë¾¾¹ıÊг¡µ÷Ë£¬µÃµ½Ä³ÖÖÔ˶¯·şµÄÔÂÏúÁ¿ y(¼ş)ÊÇÊÛ¼Û x(Ôª/¼ş)µÄÒ»´Îº¯Êı£¬ÆäÊÛ¼Û¡¢ÔÂÏúÊÛÁ¿¡¢ÔÂÏúÊÛÀûÈó w(Ôª)µÄÈı×é¶ÔÓ¦ÖµÈçÏÂ±í£º
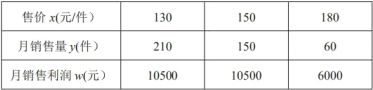
×¢£ºÔÂÏúÊÛÀûÈó£½ÔÂÏúÊÛÁ¿¡Á(ÊÛ¼ÛÒ»½ø¼Û)
£¨1£©Çó y ¹ØÓÚ x µÄº¯Êı½âÎöʽ(²»ÒªÇóĞ´³ö×Ô±äÁ¿µÄÈ¡Öµ·¶Î§)£»
£¨2£©µ±ÊÛ¼ÛÊǶàÉÙʱ£¬ÔÂÏúÊÛÀûÈó×î´ó£¿×î´óÀûÈóÊǶàÉÙÔª£¿
£¨3£©ÎªÏìÓ¦ºÅÕÙ£¬¸Ã¹«Ë¾¾ö¶¨Ã¿ÊÛ³ö 1 ¼ş·ş×°£¬¾Í¾èÔù a Ôª(a 0)£¬É̼ҹ涨¸Ã·ş×°ÊÛ¼Û²»µÃ³¬¹ı200 Ôª£¬ÔÂÏúÊÛÁ¿ÈÔÂú×ãÉϹØϵ£¬Èô´ËʱÔÂÏúÊÛ×î´óÀûÈóÈÔ¿É´ï 9600 Ôª£¬Çó a µÄÖµ£®
¡¾´ğ°¸¡¿£¨1£©y=-3x£«600£»£¨2£©µ±ÊÛ¼ÛÊÇ140Ԫʱ£¬ÔÂÏúÊÛÀûÈó×î´ó£¬×î´óÀûÈóÊÇ10800Ôª£»£¨3£©a µÄֵΪ![]()
¡¾½âÎö¡¿
£¨1£©Éèy=kx£«b£¬½«£¨130,210£©ºÍ£¨150,150£©´úÈë¼´¿ÉÇó³ö½áÂÛ£»
£¨2£©ÉèÕâÖÖÔ˶¯·şµÄ½ø¼ÛΪmÔª/¼ş£¬¸ù¾İÌâÒâ¿ÉµÃw=y£¨x£m£©£¬½«x=130£¬y=210£¬w=10500´úÈë¼´¿ÉÇó³ömµÄÖµ£¬´Ó¶øÇó³öwÓëxµÄ¶ş´Îº¯Êı¹Øϵʽ£¬×îºóÀûÓöş´Îº¯ÊıÇó×îÖµ¼´¿É£»
£¨3£©ÓÉÌâÒâ¿ÉÖª£ºw=£¨-3x£«600£©£¨x£80£a£©=-3£¨x£![]() £©2£«
£©2£«![]() £¨x¡Ü200£©£¬È»ºó¸ù¾İ¶Ô³ÆÖáÓëxµÄÈ¡Öµ·¶Î§·ÖÀàÌÖÂÛ£¬·Ö±ğ¸ù¾İ¶ş´Îº¯ÊıµÄÔö¼õĞÔÓÃxÇó³ö¶ÔÓ¦µÄ×îÖµ£¬¼´¿ÉµÃ³ö½áÂÛ£®
£¨x¡Ü200£©£¬È»ºó¸ù¾İ¶Ô³ÆÖáÓëxµÄÈ¡Öµ·¶Î§·ÖÀàÌÖÂÛ£¬·Ö±ğ¸ù¾İ¶ş´Îº¯ÊıµÄÔö¼õĞÔÓÃxÇó³ö¶ÔÓ¦µÄ×îÖµ£¬¼´¿ÉµÃ³ö½áÂÛ£®
½â£º£¨1£©ÓÉÌâÒâ¿ÉÉèy=kx£«b
½«£¨130,210£©ºÍ£¨150,150£©´úÈ룬µÃ
![]()
½âµÃ£º![]()
¡ày ¹ØÓÚ x µÄº¯Êı½âÎöʽΪy=-3x£«600
£¨2£©ÉèÕâÖÖÔ˶¯·şµÄ½ø¼ÛΪmÔª/¼ş
ÓÉÌâÒâ¿ÉÖª£ºw=y£¨x£m£©
½«x=130£¬y=210£¬w=10500´úÈ룬µÃ
10500=210£¨130£m£©
½âµÃ£ºm=80
¡àw=y£¨x£80£©=£¨-3x£«600£©£¨x£80£©=-3x2£«840x£48000=-3£¨x£140£©2£«10800
¶ø-3£¼0
¡àµ±x=140ʱ£¬wÓĞ×î´óÖµ£¬×î´óֵΪ10800
´ğ£ºµ±ÊÛ¼ÛÊÇ140Ԫʱ£¬ÔÂÏúÊÛÀûÈó×î´ó£¬×î´óÀûÈóÊÇ10800Ôª£®
£¨3£©ÓÉÌâÒâ¿ÉÖª£ºw=£¨-3x£«600£©£¨x£80£a£©=-3£¨x£![]() £©2£«
£©2£«![]() £¨x¡Ü200£©
£¨x¡Ü200£©
µ±![]() ¡İ200ʱ£¬ÓÉ-3£¼0
¡İ200ʱ£¬ÓÉ-3£¼0
¡àµ±x¡Ü200ʱ£¬wËæxµÄÔö´ó¶øÔö´ó
¡àµ±x=200ʱ£¬w×î´ó£¬´Ëʱw=0£¬¹Ê²»·ûºÏÌâÒ⣻
¡à![]() ¡Ü200£¬¼´a¡Ü120£¬ÓÉ-3£¼0
¡Ü200£¬¼´a¡Ü120£¬ÓÉ-3£¼0
µ±x=![]() £¬wÓĞ×î´óÖµ£¬´ËʱwµÄ×î´óֵΪ
£¬wÓĞ×î´óÖµ£¬´ËʱwµÄ×î´óֵΪ![]()
¼´![]()
½âµÃ£º![]() £¨²»·ûºÏÇ°ÌáÌõ¼ş£¬¹ÊÉáÈ¥£©
£¨²»·ûºÏÇ°ÌáÌõ¼ş£¬¹ÊÉáÈ¥£©
¡à![]()
´ğ£ºa µÄֵΪ![]() £®
£®

 ×ִʾäƪÓëͬ²½×÷ÎÄ´ï±êϵÁĞ´ğ°¸
×ִʾäƪÓëͬ²½×÷ÎÄ´ï±êϵÁĞ´ğ°¸ ×ß½øÎÄÑÔÎÄϵÁĞ´ğ°¸
×ß½øÎÄÑÔÎÄϵÁĞ´ğ°¸