题目内容
【题目】如图,直线 l 上有 A、B 两点,AB=12cm,点 O 是线段 AB 上的一点,OA=2OB.
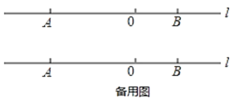
(1)OA=_______cm,OB=________cm;
(2)若点 C 是线段AB的中点,求线段 CO 的长;
(3)若动点 P、Q分别从 A、B同时出发,向右运动,点P的速度为2 厘米/秒,点Q的速度为1厘米/秒,设运动时间为x秒,当 x=_____秒时,PQ=4cm;
(4)有两条射线 OC、OD 均从射线 OA 同时绕点O顺时针方向旋转,OC旋转的速度为6度/秒,OD 旋转的速度为2度/秒.当OC与OD第一次重合时,OC、OD 同时停止旋转,设旋转时间为 t 秒,当t为何值时,射线OC⊥OD
【答案】(1)8;4;(2)OC=2cm;(3)![]() 或
或![]() ;(4)当t=22.5秒或t=67.5秒时,射线OC⊥OD.
;(4)当t=22.5秒或t=67.5秒时,射线OC⊥OD.
【解析】
(1)由OA=2OB结合AB=OA+OB=12即可求出OA、OB的长度;
(2)由点C是线段AB的中点,可求得BC的长,再根据OC=BC-OB求得OC的长;
(3)AP=4x,AQ=12+x,根据题意可列出方程:12+x-4x=4或4x-(12+x)=4,解方程求得x的值即可;
(4)当射线OC⊥OD,根据题意可列出方程6t-2t=90或270,进而得出t的值.
(1)∵AB=12cm,OA=2OB,
∴OA+OB=3OB=AB=12cm,
解得:OB=4cm,
OA=2OB=8cm.
故答案为:8;4;
(2)如图,
![]()
∵AB=12cm,C 是线段AB的中点,
∴BC=![]() =6cm,
=6cm,
∴OC=BC-OB=6-4=2cm;
(3)AP=4x,AQ=12+x,
由题意,得12+x-4x=4或4x-(12+x)=4,
解得x=![]() 或x=
或x=![]() ,
,
故答案为:![]() 或
或![]() ;
;
(4)当OC与OD第一次重合时,OC、OD同时停止旋转,
OC与OD第一次重合时所用的时间:![]() =90秒,
=90秒,
在这期间,当射线OC⊥OD,则有6t-2t=90或270,
解得t=22.5秒或t=67.5秒,
∴当t=22.5秒或t=67.5秒时,射线OC⊥OD.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
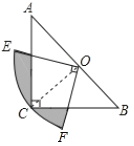
小学课堂作业系列答案【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
【题目】嘉淇同学为了探索泥茶壶盛水喝起来凉的原因,对泥茶壶和塑料壶盛水散热情况进行对比实验.在同等情况下,把稍高于室温(25.5℃)的水放入凉壶中,每隔一小时同时测出凉壶水温,所得数据如下表:
刚倒入时 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
泥茶壶 | 34 | 27 | 25 | 23.5 | 23.0 | 22.5 | 22.5 | 22.5 |
塑料壶 | 34 | 30 | 27 | 26.0 | 25.5 | 22.5 | 22.5 | 22.5 |
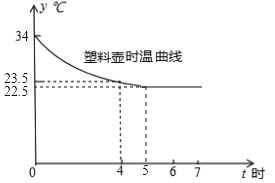
(1)塑料壶水温变化曲线如图,请在同一坐标系中,画出泥壶水温的变化曲线;
(2)比较泥壶和塑料壶水温变化情况的不同点.