Question

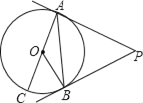
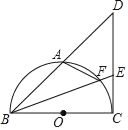
【题目】如图，BC为⊙O的直径，点A是弧BC的中点，连接BA并延长至点D，使得AD＝AB，连接CD，点E为CD上一点，连接BE交弧BC于点F，连接AF．

（1）求证：CD为⊙O的切线；

（2）求证：∠DAF＝∠BEC；

（3）若DE＝2CE＝4，求AF的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）AF＝．

【解析】

（1）欲证明CD是⊙O的切线，只要证明DC⊥BC即可；

（2）利用等角的余角相等证明即可；

（3）由△ABF∽△EBD，可得AF：DE＝AB：BE，只要求出AB，BE即可解决问题；

（1）证明：连接AC．

∵，

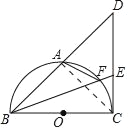
∴AB＝AC，

∵AB＝AD，

∴AC＝AB＝AD，

∴∠BCD＝90°，

∴CD⊥BC，

∴CD是⊙O的切线．

（2）解：∵BC是直径，

∴∠BAC＝∠CAD＝90°，

∴∠DAF+∠CAF＝90°，

∵∠BCE＝90°

∴∠BEC+∠CBE＝90°，

∵∠CBE＝∠CAF，

∴∠DAF＝∠BEC．

（3）解：∵AB＝BD，CA⊥BD，

∴CD＝BC，

∴△BCD是等腰直角三角形，

∴∠ACB＝∠AFB＝∠D＝45°，

∵∠ABF＝∠DBE，

∴△ABF∽△EBD，

∴AF：DE＝AB：BE，

∵DE＝2EC＝4，

∴BC＝CD＝6，AB＝3，BE＝，

∴AF＝．