题目内容
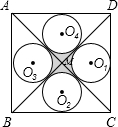
如图,正方形ABCD的对角线AC、BD交于点M,且分正方形为四个三角形,⊙O1、⊙O2、⊙O3、⊙O4分别为△AMB、△BMC、△CMD、△DMA的内切圆,已知AB=1.则⊙O1、⊙O2、⊙O3、⊙O4.所夹的中心(阴影)部分的面积为( )
A.
| B.
| C.
| D.
|

根据题意,顺次连接O1O2O3O4,
四个小圆为等圆,且四边形O1O2O3O4为正方形,
设O1O2与BD的交点E,
又AB=1,
故BD=
,BE=
,MB=
,
所以ME=
,
即小圆的半径为
,
所以O1O2=
-1,
即S正方形=3-2
,
又一四个扇形组成的面积S=(
)2π=
π,
S阴影=S正方形-S=3-2
-
π=
;
故答案为
.

四个小圆为等圆,且四边形O1O2O3O4为正方形,
设O1O2与BD的交点E,
又AB=1,
故BD=
| 2 |
| 1 |
| 2 |
| ||
| 2 |
所以ME=
| ||
| 2 |
即小圆的半径为
| ||
| 2 |
所以O1O2=
| 2 |
即S正方形=3-2
| 2 |
又一四个扇形组成的面积S=(
| ||
| 2 |
3-2
| ||
| 4 |
S阴影=S正方形-S=3-2
| 2 |
3-2
| ||
| 4 |
(4-π)(3-2
| ||
| 4 |
故答案为
(4-π)(3-2
| ||
| 4 |


练习册系列答案
相关题目






