题目内容
【题目】如图，在ABC中，AD⊥BC，垂足为D，∠B=60°，∠C=45°
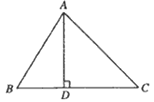
（1）求∠BAC的度数；
（2）若BD=2，求CD的长.
【答案】（1）75°；（2）2
【解析】
（1）直接根据三角形内角和定理即可求出∠BAC的度数；
（2）先利用直角三角形的性质求出AB，再根据勾股定理得到AD，然后根据∠C=45°即可得出结论．
解：（1）∵在△ABC中，∠B=60°，∠C=45°，
∴∠BAC=180°-60°-45°=75°；
（2）∵AD⊥BC，
∴∠ADB=90°，△BDC是直角三角形，
又∵∠B=60°，
∴∠BAD=30°
∴AB=2BD=4
BD2 +AD2=AB2
∴AD=2
又∵∠C=45°， ∠ADC=90°，
∴CD=AD=2.
练习册系列答案
相关题目
【题目】某校从两名优秀选手中选一名参加全市中小学运动会的男子
米跑项目，该校预先对这两名选手测试了
次，测试成绩如下表
|
|
|
|
|
|
|
| |
甲的成绩（秒） |
|
|
|
|
|
|
|
|
乙的成绩（秒） |
|
|
|
|
|
|
|
|
为了衡量这两名选手米跑的水平，你选择哪些统计量？请分别求出这些统计量的值．
你认为选派谁比较合适？为什么？
