题目内容
【题目】为美化小区环境,某小区有一块面积为30m2的等腰三角形草地,测得其一边长为10m,现要给这块三角形草地围上白色的低矮栅栏,则其长度为 m.
【答案】2![]() +10或20+2
+10或20+2![]() 或20+6
或20+6![]() .
.
【解析】
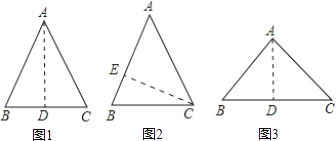
试题分析:(1)如图,当底边BC=10m时,由于S=30m2,所以高AD=6,然后根据勾股定理求出AB,AC,最后求出三角形的周长;
(2)①当△ABC是锐角三角形时,如图,当AB=AC=10m时,高CE=6m,根据勾股定理可以求出AE=8m,BE=2m,然后在RT△BEC中,可以求出BC,最后求出周长;
②当△ABC是钝角三角形时,作AD⊥BC,设BD=xm,AD=hm,求出x的长,进而可得出△ABC的周长.
解:(1)如图1,当底边BC=10m时,
由于S=30m2,所以高AD=6m,
此时AB=AC=![]() =
=![]() (m),
(m),
所以周长=(2![]() +10)m;
+10)m;
(2)①当△ABC是锐角三角形时,如图2,当AB=AC=10m时,高CE=6,此时AE=8m,BE=2m,在Rt△BEC中,BC=2![]() m,
m,
此时周长=(20+2![]() )m.
)m.
②当△ABC是钝角三角形时,如图3,设BD=xm,AD=hm,
则在Rt△ABD中,![]() ×2x×h=30,
×2x×h=30,
xh=30,
![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
故△ABC是钝角三角形时,△ABC的周长=2×10+3![]() =(20+6
=(20+6![]() )(m),
)(m),
故填空答案:2![]() +10或20+2
+10或20+2![]() 或20+6
或20+6![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
