题目内容
| |||||
答案:
解析:
解析:
|
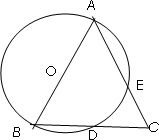
已知,如图,在△ABC中AB=AC,以AB为直径的圆交BC于点D,,交AC于点E,
求证: 证明:连接AD ∵AB是直径 ∴∠ADB=90° 2分 ∴AD⊥BC ∴∠BAD=∠CAD 4分 ∴ (2)20°20°50° 4分 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 (n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2014= .
(n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2014= .
 和y=?
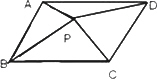
和y=? 的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是( ).
的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是( ).