题目内容
已知直线 (n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2014= .
(n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2014= .
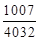
解析试题分析:用一次函数图象上点的坐标特点,直线与y轴交点坐标为(0,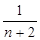 ),与x轴交点坐标为
),与x轴交点坐标为
(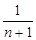 ,0)∵n>0∴
,0)∵n>0∴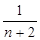 ,
,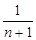 均大于0,S=
均大于0,S= ×
×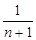 ×
×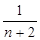 =
= (
(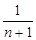 -
-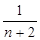 )然后利用
)然后利用
拆项法求其和即可,本题考查了一次函数图象上点的坐标特征、三角形的面积.
解答此题的难点是将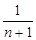 ×
×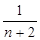 拆成
拆成 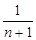 -
- 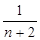 的形式.设直线与y轴相交于点A,与x轴相交于点B.
的形式.设直线与y轴相交于点A,与x轴相交于点B.
∵直线AB的解析式为:
∴当x=0时,y=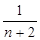 ,即OA=
,即OA=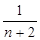 ,当y=0时,x=
,当y=0时,x=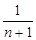 ,即OB=
,即OB=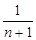 ,
,
∴Sn= OA•OB=
OA•OB= ×
×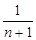 ×
× 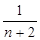 =
= (
(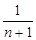 -
-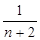 )
)
∴S1+S2+S3+…+S2014= (
( -
-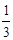 +
+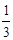 -
-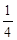 +
+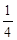 -
-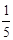 +…+
+…+ _
_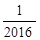 )=
)= (
( -
-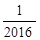 )=
)= ×
×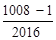 =
=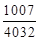
故答案为: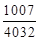
考点:一次函数图象上点的坐标特征;拆项法求和公式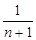 ×
×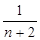 =
=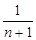 -
-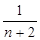 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
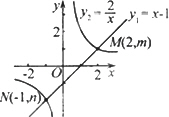
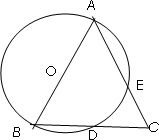
 ,
, ,
, ,…按如图所示的方式放置,点
,…按如图所示的方式放置,点 和点
和点 分别在直线
分别在直线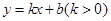 和
和 轴上,已知点
轴上,已知点 ,则
,则 的坐标是 .
的坐标是 . 
 将四边形ABCD分成面积相等的两部分,则m的值为 .
将四边形ABCD分成面积相等的两部分,则m的值为 . x的图象平行,则一次函数表达式为 。
x的图象平行,则一次函数表达式为 。 ,则输出的函数值为 .
,则输出的函数值为 .