题目内容
【题目】如图,矩形![]() 的顶点
的顶点![]() ,
,![]() 分别在菱形
分别在菱形![]() 的边
的边![]() ,
,![]() 上,顶点
上,顶点![]() 、
、![]() 在菱形
在菱形![]() 的对角线
的对角线![]() 上.
上.

(1)求证:![]() ;
;
(2)若![]() 为
为![]() 中点,
中点,![]() ,求菱形
,求菱形![]() 的周长。
的周长。
【答案】(1)证明见解析;(2)8.
【解析】
(1)根据矩形的性质得到EH=FG,EH∥FG,得到∠GFH=∠EHF,求得∠BFG=∠DHE,根据菱形的性质得到AD∥BC,得到∠GBF=∠EDH,根据全等三角形的性质即可得到结论;
(2)连接EG,根据菱形的性质得到AD=BC,AD∥BC,求得AE=BG,AE∥BG,得到四边形ABGE是平行四边形,得到AB=EG,于是得到结论.
(1)∵四边形EFGH是矩形,
∴EH=FG,EH∥FG,
∴∠GFH=∠EHF,
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE;
(2)连接EG,
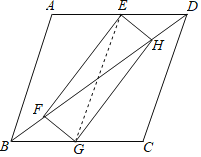
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∵E为AD中点,
∴AE=ED,
∵BG=DE,
∴AE=BG,AE∥BG,
∴四边形ABGE是平行四边形,
∴AB=EG,
∵EG=FH=2,
∴AB=2,
∴菱形ABCD的周长=8.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目