题目内容
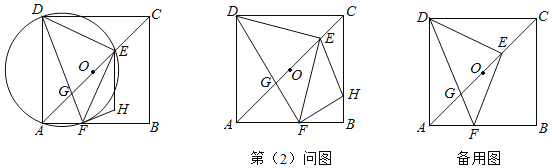
【题目】如图1和2,![]() 中,AB=3,BC=15,
中,AB=3,BC=15,![]() .点
.点![]() 为
为![]() 延长线上一点,过点
延长线上一点,过点![]() 作
作![]() 切
切![]() 于点
于点![]() ,设
,设![]() .
.
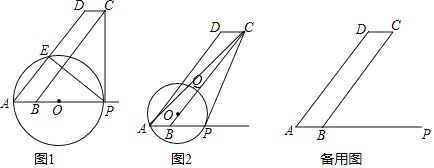
(1)如图1,![]() 为何值时,圆心
为何值时,圆心![]() 落在
落在![]() 上?若此时
上?若此时![]() 交
交![]() 于点
于点![]() ,直接指出PE与BC的位置关系;
,直接指出PE与BC的位置关系;
(2)当![]() 时,如图2,
时,如图2,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的度数,并通过计算比较弦
的度数,并通过计算比较弦![]() 与劣弧
与劣弧![]() 长度的大小;
长度的大小;
(3)当![]() 与线段
与线段![]() 只有一个公共点时,直接写出
只有一个公共点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)当x=9时,圆心O落在AP上,PE⊥BC;(2)∠CAP=45°,弦AP的长度>劣弧![]() 长度;(3)x≥18.
长度;(3)x≥18.
【解析】
(1)由三角函数定义知:Rt△PBC中,![]() tan∠PBC=tan∠DAB
tan∠PBC=tan∠DAB![]() ,设CP=4k,BP=3k,由勾股定理可求得BC,根据“直径所对的圆周角是直角”可得PE⊥AD,由此可得PE⊥BC;
,设CP=4k,BP=3k,由勾股定理可求得BC,根据“直径所对的圆周角是直角”可得PE⊥AD,由此可得PE⊥BC;
(2)作CG⊥AB,运用勾股定理和三角函数可求CG和AG,再应用三角函数求∠CAP,应用弧长公式求劣弧![]() 长度,再比较它与AP长度的大小;
长度,再比较它与AP长度的大小;
(3)当⊙O与线段AD只有一个公共点时,⊙O与AD相切于点A,或⊙O与线段DA的延长线相交于另一点,此时,BP有最小值,即x≥18.
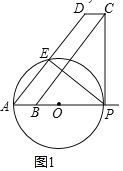
(1)如图1,AP经过圆心O.
∵CP与⊙O相切于P,∴∠APC=90°.
∵ABCD,∴AD∥BC,∴∠PBC=∠DAB,∴![]() tan∠PBC=tan∠DAB
tan∠PBC=tan∠DAB![]() ,设CP=4k,BP=3k,由CP2+BP2=BC2,得(4k)2+(3k)2=152,解得:k1=﹣3(舍去),k2=3,∴x=BP=3×3=9,故当x=9时,圆心O落在AP上;
,设CP=4k,BP=3k,由CP2+BP2=BC2,得(4k)2+(3k)2=152,解得:k1=﹣3(舍去),k2=3,∴x=BP=3×3=9,故当x=9时,圆心O落在AP上;
∵AP是⊙O的直径,∴∠AEP=90°,∴PE⊥AD.
∵ABCD,∴BC∥AD,∴PE⊥BC.
(2)如图2,过点C作CG⊥AP于G.
∵ABCD,∴BC∥AD,∴∠CBG=∠DAB,∴![]() tan∠CBG=tan∠DAB
tan∠CBG=tan∠DAB![]() ,设CG=4m,BG=3m,由勾股定理得:(4m)2+(3m)2=152,解得:m=3,∴CG=4×3=12,BG=3×3=9,PG=BG﹣BP=9﹣4=5,AP=AB+BP=3+4=7,∴AG=AB+BG=3+9=12,∴tan∠CAP
,设CG=4m,BG=3m,由勾股定理得:(4m)2+(3m)2=152,解得:m=3,∴CG=4×3=12,BG=3×3=9,PG=BG﹣BP=9﹣4=5,AP=AB+BP=3+4=7,∴AG=AB+BG=3+9=12,∴tan∠CAP![]() 1,∴∠CAP=45°;
1,∴∠CAP=45°;
连接OP,OQ,过点O作OH⊥AP于H,则∠POQ=2∠CAP=2×45°=90°,PH![]() AP
AP![]() .
.
在Rt△CPG中,![]() 13.
13.
∵CP是⊙O的切线,∴∠OPC=∠OHP=90°,∠OPH+∠CPG=90°,∠PCG+∠CPG=90°,∴∠OPH=∠PCG,∴△OPH∽△PCG,∴![]() ,即PH×CP=CG×OP,
,即PH×CP=CG×OP,![]() 13=12OP,∴OP
13=12OP,∴OP![]() ,∴劣弧
,∴劣弧![]() 长度
长度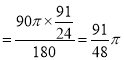 .
.
∵![]() 2π<7,∴弦AP的长度>劣弧
2π<7,∴弦AP的长度>劣弧![]() 长度.
长度.
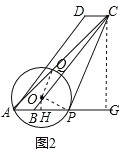
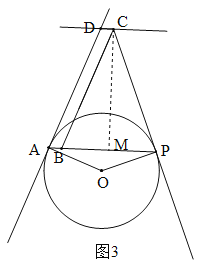
(3)当⊙O与线段AD只有一个公共点时,⊙O与AD相切于点A,或⊙O与线段DA的延长线相交于另一点,此时圆心O位于直线AB下方,且∠OAD≥90°,当∠OAD=90°,∠CPM=∠DAB时,即⊙O与DA切于点A时,BP取得最小值,如图3,过点C作CM⊥AB于M.
∵∠DAB=∠CBP,∴∠CPM=∠CBP,∴CB=CP.
∵ABCD,∴AD∥BC,∴∠PBC=∠DAB,∴tan∠PBC=tan∠DAB![]() ,设CM=4k,BM=3k,由CM2+BM2=BC2,得(4k)2+(3k)2=152,解得:k1=﹣3(舍去),k2=3,∴x=BM=3×3=9.
,设CM=4k,BM=3k,由CM2+BM2=BC2,得(4k)2+(3k)2=152,解得:k1=﹣3(舍去),k2=3,∴x=BM=3×3=9.
∵CM⊥AB,∴BP=2BM=2×9=18,∴x≥18.

 阅读快车系列答案
阅读快车系列答案