Question

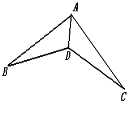
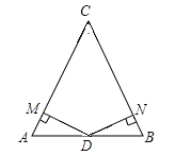
【题目】如图，在△ABC中，D是AB的中点，DM⊥AC于点M,DN⊥BC于点N,且DM=DN.

（1）求证：AM=BN;

（2）AC=BC.

Answer 1

【答案】（1）见解析;（2）见解析.

【解析】

对于（1），连接CD，利用HL定理，先证明△DAM≌△DBN，再由全等三角形对应边相等求得结论；
对于（2），由DM=DN且DM⊥AC于M，DN⊥BC于N，可证得Rt△CDM≌Rt△CDN，则CM=CN，再由（1）的结论即可得证.

证明：（1）连接CD，如图所示，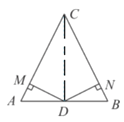

∵D是AB的中点，
∴AD=BD.
又∵DM=DN且DM⊥AC于M，DN⊥BC于N，
∴△DAM≌△DBN（HL），
∴AM=BN.
（2）∵DM=DN且DM⊥AC于M，DN⊥BC于N，
∴Rt△CDM≌Rt△CDN（HL），
∴CM=CN，
∴AC=AM+CM，BC=BN+CN，
∴AC=BC.