��Ŀ����
����Ŀ����ͼ����֪���κ���L��y��mx2+2mx+k������m��k�dz�����kΪ����������
��1����L�����㣨1��k+6������m��ֵ��
��2����m��2����L��x���й�����ʱ�ҹ�����ĺ�����Ϊ�����������ȷ��k��ֵ��
��3���ڣ�2���������½�L��y��mx2+2mx+k��ͼ������ƽ��8����λ���õ�����ͼ��M����M�Ľ���ʽ��
��4����M��ͼ����x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ��N�������µ�ͼ�������⣬��ֱ��y��![]() x+b��N������������ʱ����ֱ��д��b��ȡֵ��Χ��
x+b��N������������ʱ����ֱ��д��b��ȡֵ��Χ��

���𰸡���1��m��2����2��k��2����3��y��2x2+4x��6������4����![]() ��b��
��b��![]() ��b��
��b��![]() ��
��
��������
��1�����㣨1��k+6������y��mx2+2mx+k��������⣻
��2��������ã�����16��8k��0��������⣻
��3������ƽ�ƵĹ�ʽ������⣻
��4��ȷ����H��A��B�����ٽ�㣬����ٽ��ʱb��ֵ��������⣮
�⣺��1�����㣨1��k+6������y��mx2+2mx+k����ã�
m��2��
��2��y��mx2+2mx+k��2x2+4x+k��
������ã�����16��8k��0����ã�k��2��
��kΪ����������k��1ʱ������û�������⣬����ȥ��
��k��2��
��3����m��2��k��2ʱ��y��2x2+4x+2������ƽ��8����λ��
ƽ�ƺ�ı���ʽΪ��y��2x2+4x+2��8��2x2+4x��6��
��4���ɣ�3��֪��M�ı���ʽΪ��y��2x2+4x��6����
���ۺ������ߵı���ʽΪ��y�䣽��2x2��4x+6����
��ֱ��mΪ��y��![]() x+b����
x+b����
����ֱ��m�뷭�ۺ��ͼ����һ�����㣨��H��ʱ������ͼ��
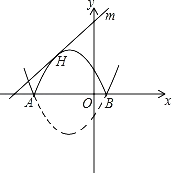
�����ڢ��������ã�2x2+![]() x+b��6��0��
x+b��6��0��
�����![]() ��8��b��6����0����ã�b��
��8��b��6����0����ã�b��![]() ��
��
����ֱ��m����A����3��0��ʱ��
����A�����������ʽ�ã�0��![]() ������3��+b����ã�b��
������3��+b����ã�b��![]() ��
��
����ֱ��m����Bʱ��
ͬ���ɵã�b����![]() ��
��
��ֱ��y��![]() x+b��N������������ʱ��b��ȡֵ��ΧΪ����
x+b��N������������ʱ��b��ȡֵ��ΧΪ����![]() ��b��
��b��![]() ��b��
��b��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ���ڿ����¹ڷ��������ڼ䣬�ϰ���Խ��Խ��������������ȡ��Ҫ���������ϣ�Сʯ��Ӫ��ˮ����Ҳ��ʱ������ij����ƽ̨���������۵�ˮ���еIJ��֣����±������д��������������ˮ�������ͷ���һ�ι���ˮ�����ܼ���128Ԫ��![]() Ԫ��ÿ�ʶ����˿�����֧���ɹ���Сʯ��õ�֧�����80%��
Ԫ��ÿ�ʶ����˿�����֧���ɹ���Сʯ��õ�֧�����80%��
�������ˮ�� | |
ˮ�� | ����ǰ���� |
ƻ�� | 58Ԫ/�� |
�ҰҸ� | 70Ԫ/�� |
������ | 100Ԫ/�� |
������ | 48Ԫ/�� |
��1����![]() ʱ��ij�˿�һ�ι���ƻ���ͳ����Ӹ�1�䣬��Ҫ֧��_____Ԫ��Сʯ��õ�______Ԫ��
ʱ��ij�˿�һ�ι���ƻ���ͳ����Ӹ�1�䣬��Ҫ֧��_____Ԫ��Сʯ��õ�______Ԫ��
��2���ڴ�����У�Ϊ����Сʯÿ�ʶ������õ��Ľ����ڴ���ǰ�ܼ۵����ۣ���![]() �����ֵΪ_____��
�����ֵΪ_____��