题目内容
【题目】已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且OC=3OA.

(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
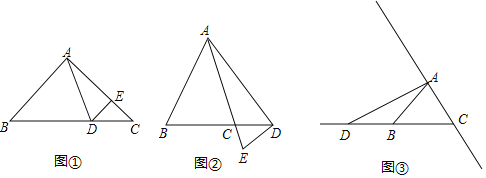
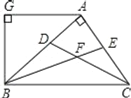
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
【答案】(1)y=x2-2x-3 ;
(2)直线BC的函数表达式为y=x-3;
(3)①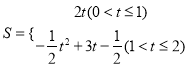
②当t =2秒时,S有最大值,最大值为![]() .
.
(4)存在符合条件的点M,且坐标为M 1(-![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ), M3(
), M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() )
)
【解析】分析:(1)先由OC、OA的数量关系确定点C的坐标,然后利用待定系数法可求出抛物线的解析式; (2)由(1)的抛物线解析式可得点B的坐标,结合点C的坐标,利用待定系数法求解即可; (3)①首先要明确正方形ODEF和△OBC重合部分的形状:当点D在△OBC内部时,两者的重合部分是矩形;当点D在△OBC外部时,两者的重合部分是五边形,其面积可由正方形的面积减去△ 的面积(G、H分别为 、 和线段BC的交点).在判断t的取值范围时,要注意一个“关键点”即点D位于线段BC上时; ②根据①的函数性质即可得到答案. (4)若存在以A、M、N、P为顶点的平行四边形,应分AM PN或AN PM两种情况.由于AM在x轴上,结合平行四边形的特点可知:无论哪种情况,点N到x轴的距离都等于点P到x轴的距离,根据这个特点可确定点M、N的坐标.
本题解析:(1)∵ A(-1,0), ![]() ,C(0,-3)
,C(0,-3)
∵抛物线经过A(-1,0),C(0,-3)
∴![]() ,∴
,∴![]() ,
,
∴y=x2-2x-3
(2)由(1)的抛物线解析式可知:点B(3,0).
设直线BC的解析式为y=kx+b.
将B(3,0),C(0,-3)代入得![]() ,解得
,解得![]() ,
,
∴直线BC的函数表达式为y=x-3.
(3)当正方形ODEF的顶点D运动到直线BC上时,设D点的坐标为(m,-2),
根据题意得: -2=m-3,∴m=1
①当0<t≤1时,S1=2t
当1<t≤2时
S2=![]() =2t-
=2t-![]()
=-![]() ,
,
②当t =2秒时,S有最大值,最大值为![]()
(4)由(2)知:点P(1,-2),假设存在符合条件的点M.
①当AM∥PN,AM=PN时,点N、P的纵坐标相同,
即点N的纵坐标为-2,代入抛物线的解析式中得x-2x-3=-2,
解得 x=1±![]() ,
,
∴AM=NP=![]() ,
,
∴M 1(-![]() ,0) M2(
,0) M2(![]() ,0),
,0),
②当AN∥PM,AN=PM时,平行四边形的对角线PN、AM互相平分.
设M(m,0),则N(m-2,2).
将点N的坐标代入抛物线的解析式中,得(m-2)-2(m-2)-3=2,
解得 m=3±![]() ,
,
∴M3(3-![]() ,0) M4(3+
,0) M4(3+![]() ,0 ).
,0 ).
综上,存在符合条件的M点,且坐标为:
M 1(-![]() ,0) M2(
,0) M2(![]() ,0)
,0)
M3(3-![]() ,0) M4(3+
,0) M4(3+![]() ,0 )
,0 )