题目内容
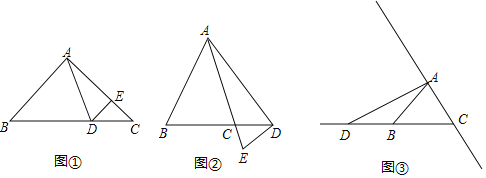
【题目】如图①，在△ABC中，∠B＝∠C，点D在BC边上，点E在AC边上，且∠ADE＝∠AED，连结DE．
（1）若∠BAC＝100°，∠DAE＝40°，则∠CDE＝ ，此时
＝ ；
（2）若点D在BC边上（点B、C除外）运动，试探究∠BAD与∠CDE的数量关系并说明理由；
（3）若点D在线段BC的延长线上，点E在线段AC的延长线上（如图②），其余条件不变，请直接写出∠BAD与∠CDE的数量关系： ；
（4）若点D在线段CB的延长线上（如图③）、点E在直线AC上，∠BAD＝26°，其余条件不变，则∠CDE＝ °（友情提醒：可利用图③画图分析）
【答案】（1）30°，2；（2）∠BAD＝2∠CDE；理由见解析；（3）∠BAD＝2∠CDE ；（4）∠CDE＝13或77°
【解析】
（1）根据三角形内角和与三角形外角的性质可得结论；
（2）设∠DAE＝x，∠BAC＝y，同理可得∠BAD与∠CDE的数量关系；
（3）设∠DAE＝x，∠BAC＝y，同理可得∠BAD与∠CDE的数量关系；
（4）分两种情况讨论，同理可计算∠CDE的度数．
解：（1）如图，
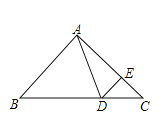
∵∠DAE＝40°，∠ADE＝∠AED，
∴∠ADE＝70°，
∵∠BAC＝100°，
∴∠BAD＝∠BAC﹣∠DAE＝100°﹣40°＝60°，
∵∠B＝∠C＝40°，
∴∠ADC＝∠B+∠BAD＝40°+60°＝100°，
∴∠CDE＝30°，
∴
＝2，
故答案为：30°，2；
（2）如图，∠BAD与∠CDE的数量关系是：∠BAD＝2∠CDE；
理由是：设∠DAE＝x，∠BAC＝y，则∠BAD＝y﹣x，
∵∠DAE＝x，∠ADE＝∠AED，
∴∠ADE＝
，
∵∠B＝∠C＝
，
∴∠ADC＝∠B+∠BAD＝+y﹣x＝90°+
y﹣x，
∴∠CDE＝∠ADC﹣∠ADE＝90°+y﹣x﹣＝
，
∴∠BAD＝2∠CDE；
（3）如图，∠BAD与∠CDE的数量关系：∠BAD＝2∠CDE，
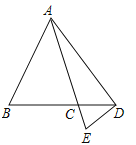
理由是：设∠DAE＝x，∠BAC＝y，则∠BAD＝x+y，
∵∠DAE＝x，∠ADE＝∠AED，
∴∠ADE＝∠E＝，
∵∠B＝，
∴∠ACD＝∠B+∠BAC＝∠E+∠CDE，
∴+y＝+∠CDE，
∴∠CDE＝（x+y），
∴∠BAD＝2∠CDE；
故答案为：∠BAD＝2∠CDE；
（4）分两种情况：
①当E在射线CA上时，如图所示，
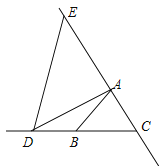
设∠DAE＝x，∠BAC＝y，则x+y＝180°﹣26°＝154°，
∵∠DAE＝x，∠ADE＝∠AED，
∴∠AED＝，
∵∠C＝，
△CDE中，∠CDE＝180°﹣∠AED﹣∠C＝180°﹣﹣＝（x+y）＝
＝77°
②当E在射线AC上时，如图所示，
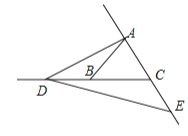
设∠DAE＝x，∠BAC＝y，则x﹣y＝26°，
∵∠DAE＝x，∠ADE＝∠AED，
∴∠AED＝，
∵∠ACB＝，
△CDE中，∠CDE＝∠ACB﹣∠AED＝﹣＝（x﹣y）＝
＝13°，
综上，∠CDE＝13°或77°；
故答案为：13或77．
