Question

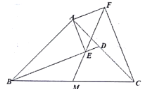
【题目】如图，AB 是⊙M 的直径，BC 是⊙M 的切线，切点为 B，C 是 BC 上（除 B 点外）的任意一点，连接 CM 交⊙M 于点 G，过点 C 作 DC⊥BC 交 BG 的 延长线于点 D，连接 AG 并延长交 BC 于点 E．

（1）求证：△ABE∽△BCD；

（2）若 MB=BE=1，求 CD 的长度．

Answer 1

【答案】（1）证明见解析；（2）CD=

【解析】

（1）根据直径所对圆周角是直角和切线的性质，即可证明三角形相似；

（2）利用勾股定理和面积法得到 AG、GE，根据三角形相似求得 GH，得到 MB、GH 和 CD 的数量关系，求得 CD的长即可．

（1）∵BC 为⊙M 切线，

∴∠ABC=90°，

∵DC⊥BC，

∴∠BCD=90°，

∴∠ABC=∠BCD，

∵AB 是⊙M 的直径，

∴∠AGB=90°，

即：BG⊥AE，

∴∠CBD=∠A，

∴△ABE∽△BCD；

（2）过点 G 作 GH⊥BC 于 H，

∵MB=BE=1∴AB=2，

∴AE=，

由（1）根据面积法 ABBE=BGAE，

∴BG=，

由勾股定理：AG=，GE=，

∵GH∥AB，

∴，

∴，

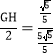∴GH=，

又∵GH∥AB，

∴① ，

同理：②，

①+②，得 ，

∴ ，

∴CD=.