��Ŀ����
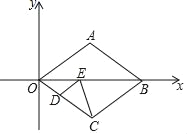
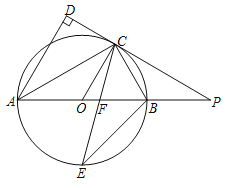
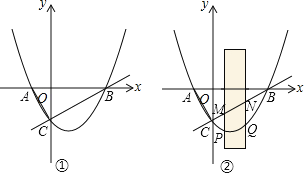
����Ŀ����ͼ�٣�ֱ��y��![]() ��x�ᡢy��ֱ��ڵ�B��C��������y��
��x�ᡢy��ֱ��ڵ�B��C��������y��![]() ��B��C���㣬����x�����һ������Ϊ��A������AC��
��B��C���㣬����x�����һ������Ϊ��A������AC��
��1���������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�D�����A���غϣ���ʹ��S��DBC��S��ABC�������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
��3���п���Ϊ2�������㹻���ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��CB�ڵ�M�͵�N���ھ���ƽ�ƹ����У����Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ�����M�����꣮
���𰸡���1��![]() ����2�����ڣ���D��8��5�������ɼ���������3����M������Ϊ��2����2����2+2
����2�����ڣ���D��8��5�������ɼ���������3����M������Ϊ��2����2����2+2![]() ��
��![]() ��2����2��2
��2����2��2![]() ����
����![]() ��2��
��2��
��������
��1�����ô���ϵ�������ɽ�����⣮
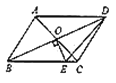
��2����ͼ���У���AD��BC����������D����S��ABC=S��BCD�����ֱ��AD�Ľ���ʽ������������ȷ�����꼴�ɣ�
��3����M��m��![]() m-3������N��m+2��
m-3������N��m+2��![]() m-2�����ɵ�P��m��
m-2�����ɵ�P��m��![]() m2-m-3����Q[m+2��
m2-m-3����Q[m+2��![]() ��m+2��2-��m+2��-3]���Ƴ�PM=
��m+2��2-��m+2��-3]���Ƴ�PM=![]() m-3-��
m-3-��![]() m2-m-3����NQ=
m2-m-3����NQ=![]() m-2-[
m-2-[![]() ��m+2��2-��m+2��-3]����PM=QNʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ��ɴ˹������̼��ɽ�����⣮
��m+2��2-��m+2��-3]����PM=QNʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ��ɴ˹������̼��ɽ�����⣮
��1��������C��0����3����B��6��0������C��0����3����B��6��0������y��![]() +bx+c�õ�
+bx+c�õ�![]() �����
�����![]() ���������ߵĽ���ʽΪy��
���������ߵĽ���ʽΪy��![]() x2��x��3��
x2��x��3��
��2����ͼ���У���AD��BC����������D����S��ABC��S��BCD��
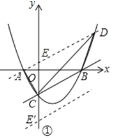
��ֱ��BC�Ľ���ʽΪy��![]() x��3��A����2��0������ֱ��AD�Ľ���ʽΪy��
x��3��A����2��0������ֱ��AD�Ľ���ʽΪy��![]() x+1����
x+1����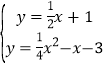 �����
�����![]() ��
��![]() ����D��8��5����
����D��8��5����
��ֱ��AD��y����E��0��1������E���ڵ�C�ĶԳƵ�E����0����7����
�����E��ƽ��BC��ֱ�ߵĽ���ʽΪy��![]() x��7����
x��7����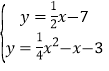 ���������⣬
���������⣬
����ֱ��BC���·����������������ĵ�D�������������ĵ�D��8��5����
��3����M��m��![]() m��3������N��m+2��
m��3������N��m+2��![]() m��2����
m��2����
��P��m��![]() m2��m��3����Q[m+2��
m2��m��3����Q[m+2��![]() ��m+2��2����m+2����3]��
��m+2��2����m+2����3]��
��PM��![]() m��3����
m��3����![]() m2��m��3����NQ��
m2��m��3����NQ��![]() m��2��[
m��2��[![]() ��m+2��2����m+2����3]��
��m+2��2����m+2����3]��
��PM��QNʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
��|![]() m��3����
m��3����![]() m2��m��3��|��|
m2��m��3��|��|![]() m��2��[
m��2��[![]() ��m+2��2����m+2����3]|��ã�m��2��2��2
��m+2��2����m+2����3]|��ã�m��2��2��2![]() ��
��
�����������ĵ�M������Ϊ��2����2����2+2![]() ��
��![]() ��2����2��2
��2����2��2![]() ����
����![]() ��2����
��2����