ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏyΘΫ©¹![]() x2©¹
x2©¹![]() x+2”κx÷αΫΜ”ΎΒψAΘ§BΝΫΒψΘ§ΫΜy÷α”ΎCΒψΘ§≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κx÷αΫΜ”ΎHΒψΘ§Ζ÷±π“‘OCΓΔOAΈΣ±ΏΉςΨΊ–ΈAECOΘ°
x+2”κx÷αΫΜ”ΎΒψAΘ§BΝΫΒψΘ§ΫΜy÷α”ΎCΒψΘ§≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κx÷αΫΜ”ΎHΒψΘ§Ζ÷±π“‘OCΓΔOAΈΣ±ΏΉςΨΊ–ΈAECOΘ°
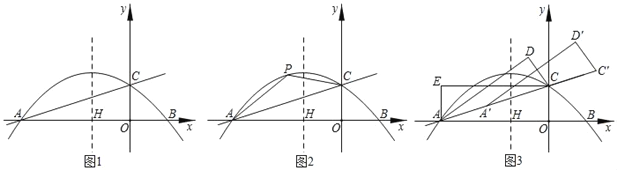
Θ®1Θ©«σ÷±œΏACΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦ2Θ§PΈΣ÷±œΏAC…œΖΫ≈ΉΈοœΏ…œΒΡ»Έ“β“ΜΒψΘ§‘ΎΕ‘≥Τ÷α…œ”–“ΜΕ·ΒψMΘ§Β±ΥΡ±Ώ–ΈAOCPΟφΜΐΉν¥σ ±Θ§«σ|PM©¹OM|ΒΡΉν¥σ÷ΒΘ°
Θ®3Θ©»γΆΦ3Θ§ΫΪΓςAOC―Ί÷±œΏACΖ≠’έΒΟΓςACDΘ§‘ΌΫΪΓςACD―ΊΉ≈÷±œΏACΤΫ“ΤΒΟΓςA'CΓδD'Θ° ΙΒΟΒψAΓδΓΔC'‘Ύ÷±œΏAC…œΘ§ «Ζώ¥φ‘Ύ’β―υΒΡΒψDΓδΘ§ ΙΒΟΓςAΓδEDΓδΈΣ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψDΓδΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ(1) yΘΫ![]() x+2ΘΜ(2) ΒψMΉχ±ξΈΣΘ®©¹2Θ§
x+2ΘΜ(2) ΒψMΉχ±ξΈΣΘ®©¹2Θ§![]() Θ© ±Θ§ΥΡ±Ώ–ΈAOCPΒΡΟφΜΐΉν¥σΘ§¥Υ ±|PM©¹OM|”–Ήν¥σ÷Β
Θ© ±Θ§ΥΡ±Ώ–ΈAOCPΒΡΟφΜΐΉν¥σΘ§¥Υ ±|PM©¹OM|”–Ήν¥σ÷Β![]() ΘΜ (3)¥φ‘ΎΘ§DΓδΉχ±ξΈΣΘΚΘ®0Θ§4Θ©ΜρΘ®©¹6Θ§2Θ©ΜρΘ®
ΘΜ (3)¥φ‘ΎΘ§DΓδΉχ±ξΈΣΘΚΘ®0Θ§4Θ©ΜρΘ®©¹6Θ§2Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΝνxΘΫ0Θ§‘ρyΘΫ2Θ§ΝνyΘΫ0Θ§‘ρxΘΫ2Μρ©¹6Θ§«σ≥ωΒψAΓΔBΓΔCΉχ±ξΘ§Φ¥Ω…«σΫβΘΜ
Θ®2Θ©Ν§Ϋ”OPΫΜΕ‘≥Τ÷α”ΎΒψMΘ§¥Υ ±Θ§|PM©¹OM|”–Ήν¥σ÷ΒΘ§Φ¥Ω…«σΫβΘΜ
Θ®3Θ©¥φ‘ΎΘΜΖ÷ΔΌAΓδDΓδΓΆAΓδEΘΜΔΎAΓδDΓδΓΆEDΓδΘΜΔέEDΓδΓΆAΓδE»ΐ÷÷«ιΩωάϊ”ΟΙ¥Ι…Ε®άμΝ–ΖΫ≥Χ«σΫβΦ¥Ω…Θ°
Θ®1Θ©ΝνxΘΫ0Θ§‘ρyΘΫ2Θ§ΝνyΘΫ0Θ§‘ρxΘΫ2Μρ©¹6Θ§ΓύAΘ®©¹6Θ§0Θ©ΓΔBΘ®2Θ§0Θ©ΓΔCΘ®0Θ§2Θ©Θ§Κ· ΐΕ‘≥Τ÷αΈΣΘΚxΘΫ©¹2Θ§ΕΞΒψΉχ±ξΈΣΘ®©¹2Θ§![]() Θ©Θ§CΒψΉχ±ξΈΣΘ®0Θ§2Θ©Θ§‘ρΙΐΒψCΒΡ÷±œΏ±μ¥ο ΫΈΣΘΚyΘΫkx+2Θ§ΫΪΒψAΉχ±ξ¥ζ»κ…œ ΫΘ§ΫβΒΟΘΚk
Θ©Θ§CΒψΉχ±ξΈΣΘ®0Θ§2Θ©Θ§‘ρΙΐΒψCΒΡ÷±œΏ±μ¥ο ΫΈΣΘΚyΘΫkx+2Θ§ΫΪΒψAΉχ±ξ¥ζ»κ…œ ΫΘ§ΫβΒΟΘΚk![]() Θ§‘ρΘΚ÷±œΏACΒΡ±μ¥ο ΫΈΣΘΚy
Θ§‘ρΘΚ÷±œΏACΒΡ±μ¥ο ΫΈΣΘΚy![]() x+2ΘΜ
x+2ΘΜ
Θ®2Θ©»γΆΦΘ§ΙΐΒψPΉςx÷αΒΡ¥ΙœΏΫΜAC”ΎΒψHΘ°
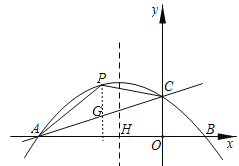
ΥΡ±Ώ–ΈAOCPΟφΜΐΘΫΓςAOCΒΡΟφΜΐ+ΓςACPΒΡΟφΜΐΘ§ΥΡ±Ώ–ΈAOCPΟφΜΐΉν¥σ ±Θ§÷Μ–η“ΣΓςACPΒΡΟφΜΐΉν¥σΦ¥Ω…Θ§…ηΒψPΉχ±ξΈΣΘ®mΘ§![]() m2
m2![]() m+2Θ©Θ§‘ρΒψGΉχ±ξΈΣΘ®mΘ§
m+2Θ©Θ§‘ρΒψGΉχ±ξΈΣΘ®mΘ§![]() m+2Θ©Θ§SΓςACP
m+2Θ©Θ§SΓςACP![]() PGOA
PGOA![]() Θ®
Θ®![]() m2
m2![]() m+2
m+2![]() m©¹2Θ©6
m©¹2Θ©6![]() m2©¹3mΘ§Β±mΘΫ©¹3 ±Θ§…œ Ϋ»ΓΒΟΉν¥σ÷ΒΘ§‘ρΒψPΉχ±ξΈΣΘ®©¹3Θ§
m2©¹3mΘ§Β±mΘΫ©¹3 ±Θ§…œ Ϋ»ΓΒΟΉν¥σ÷ΒΘ§‘ρΒψPΉχ±ξΈΣΘ®©¹3Θ§![]() Θ©Θ°Ν§Ϋ”OPΫΜΕ‘≥Τ÷α”ΎΒψMΘ§¥Υ ±Θ§|PM©¹OM|”–Ήν¥σ÷ΒΘ§÷±œΏOPΒΡ±μ¥ο ΫΈΣΘΚy
Θ©Θ°Ν§Ϋ”OPΫΜΕ‘≥Τ÷α”ΎΒψMΘ§¥Υ ±Θ§|PM©¹OM|”–Ήν¥σ÷ΒΘ§÷±œΏOPΒΡ±μ¥ο ΫΈΣΘΚy![]() xΘ§Β±xΘΫ©¹2 ±Θ§y
xΘ§Β±xΘΫ©¹2 ±Θ§y![]() Θ§Φ¥ΘΚΒψMΉχ±ξΈΣΘ®©¹2Θ§
Θ§Φ¥ΘΚΒψMΉχ±ξΈΣΘ®©¹2Θ§![]() Θ©Θ§|PM©¹OM|ΒΡΉν¥σ÷ΒΈΣΘΚ
Θ©Θ§|PM©¹OM|ΒΡΉν¥σ÷ΒΈΣΘΚ![]() =
=![]() Θ°
Θ°
Θ®3Θ©¥φ‘ΎΘ°
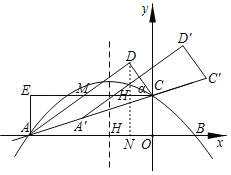
ΓΏAEΘΫCDΘ§ΓœAECΘΫΓœADCΘΫ90ΓψΘ§ΓœEMAΘΫΓœDMCΘ§ΓύΓςEAMΓ’ΓςDCMΘ®AASΘ©Θ§ΓύEMΘΫDMΘ§AMΘΫMCΘ§…ηΘΚEMΘΫaΘ§‘ρΘΚMCΘΫ6©¹aΘ°‘ΎRtΓςDCM÷–Θ§”…Ι¥Ι…Ε®άμΒΟΘΚMC2ΘΫDC2+MD2Θ§Φ¥ΘΚΘ®6©¹aΘ©2ΘΫ22+a2Θ§ΫβΒΟΘΚa![]() Θ§‘ρΘΚMC
Θ§‘ρΘΚMC![]() Θ§ΙΐΒψDΉςx÷αΒΡ¥ΙœΏΫΜx÷α”ΎΒψNΘ§ΫΜEC”ΎΒψHΘ°‘ΎRtΓςDMC÷–Θ§
Θ§ΙΐΒψDΉςx÷αΒΡ¥ΙœΏΫΜx÷α”ΎΒψNΘ§ΫΜEC”ΎΒψHΘ°‘ΎRtΓςDMC÷–Θ§![]() DHMC
DHMC![]() MDDCΘ§Φ¥ΘΚDH
MDDCΘ§Φ¥ΘΚDH![]() 2Θ§‘ρΘΚDH
2Θ§‘ρΘΚDH![]() Θ§HC
Θ§HC![]() Θ§Φ¥ΘΚΒψDΒΡΉχ±ξΈΣΘ®
Θ§Φ¥ΘΚΒψDΒΡΉχ±ξΈΣΘ®![]() Θ©ΘΜ
Θ©ΘΜ
…ηΘΚΓςACD―ΊΉ≈÷±œΏACΤΫ“ΤΝΥmΗωΒΞΈΜΘ§‘ρΘΚΒψAΓδΉχ±ξΘ®©¹6![]() Θ©Θ§ΒψDΓδΉχ±ξΈΣΘ®
Θ©Θ§ΒψDΓδΉχ±ξΈΣΘ®![]() Θ©Θ§ΕχΒψEΉχ±ξΈΣΘ®©¹6Θ§2Θ©Θ§‘ρ
Θ©Θ§ΕχΒψEΉχ±ξΈΣΘ®©¹6Θ§2Θ©Θ§‘ρ![]() =
=![]() =36Θ§
=36Θ§![]() =
=![]() =
=![]() Θ§
Θ§![]() =
=![]() =
=![]() Θ°»τΓςAΓδEDΓδΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§Ζ÷»ΐ÷÷«ιΩωΧ÷¬έΘΚ
Θ°»τΓςAΓδEDΓδΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§Ζ÷»ΐ÷÷«ιΩωΧ÷¬έΘΚ
ΔΌΒ±![]() +
+![]() =
=![]() ±Θ§36+
±Θ§36+![]() =
=![]() Θ§ΫβΒΟΘΚm=
Θ§ΫβΒΟΘΚm=![]() Θ§¥Υ ±DΓδΘ®
Θ§¥Υ ±DΓδΘ®![]() Θ©ΈΣΘ®0Θ§4Θ©ΘΜ
Θ©ΈΣΘ®0Θ§4Θ©ΘΜ
ΔΎΒ±![]() +
+![]() =
=![]() ±Θ§36+
±Θ§36+![]() =
=![]() Θ§ΫβΒΟΘΚm=
Θ§ΫβΒΟΘΚm=![]() Θ§¥Υ ±DΓδΘ®
Θ§¥Υ ±DΓδΘ®![]() Θ©ΈΣΘ®Θ≠6Θ§2Θ©ΘΜ
Θ©ΈΣΘ®Θ≠6Θ§2Θ©ΘΜ
ΔέΒ±![]() +
+![]() =
=![]() ±Θ§
±Θ§![]() +
+![]() =36Θ§ΫβΒΟΘΚm=
=36Θ§ΫβΒΟΘΚm=![]() Μρm=
Μρm=![]() Θ§¥Υ ±DΓδΘ®
Θ§¥Υ ±DΓδΘ®![]() Θ©ΈΣΘ®Θ≠6Θ§2Θ©ΜρΘ®
Θ©ΈΣΘ®Θ≠6Θ§2Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
Ήέ…œΥυ ωΘΚDΉχ±ξΈΣΘΚΘ®0Θ§4Θ©ΜρΘ®©¹6Θ§2Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°