题目内容
【题目】如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则(1)BP![]() cm,BQ
cm,BQ![]() cm.(用含t的代数式表示)
cm.(用含t的代数式表示)
(2)当t为何值时,△PBQ是直角三角形?
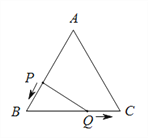
【答案】(1)3-t,t;(2)当t=1s或t=2s时,△PBQ是直角三角形.
【解析】分析:(1)根据路程=速度×时间即可求得;(2)根据等边三角形的性质可以知道这个直角三角形∠B=60°,所以就可以表示出BQ与PB的关系,要分情况进行讨论:①∠BPQ=90°;②∠PQB=90°.然后在直角三角形BQP中根据BP,BQ的表达式和∠B的度数进行求解即可.
本题解析:
(1)![]() cm,
cm,![]() cm
cm
在 △PBQ中,![]()
若△PBQ是直角三角形,则点P或点Q
为直角顶点
①若点P为直角顶点,因为![]() ,所以
,所以![]()
所以![]() 即t=2(3-t), 解得t=2
即t=2(3-t), 解得t=2
②若点Q是直角顶点,∵![]() ,∴
,∴![]()
∴![]() 即3-t=2t, 解得t=1
即3-t=2t, 解得t=1
答:当t=1s或t=2s时,△PBQ是直角三角形

练习册系列答案
相关题目