题目内容
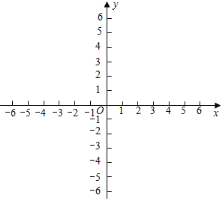
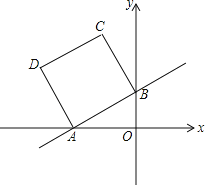
【题目】如图所示,在平面直角坐标系中,已知一次函数y=![]() x+1的图象与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD.
x+1的图象与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD.
(1)求边AB的长;
(2)求点C,D的坐标;
(3)在x轴上是否存在点M,使△MDB的周长最小?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)C(﹣1,3),D(﹣3,2);(3)M(﹣1,0).
;(2)C(﹣1,3),D(﹣3,2);(3)M(﹣1,0).
【解析】
试题分析:(1)在直角三角形AOB中,由OA与OB的长,利用勾股定理求出AB的长即可;
(2)过C作y轴垂线,过D作x轴垂线,分别交于点E,F,可得三角形CBE与三角形ADF与三角形AOB全等,利用全等三角形对应边相等,确定出C与D坐标即可;
(3)作出B关于x轴的对称点B′,连接B′D,与x轴交于点M,连接BD,BM,此时△MDB周长最小,求出此时M的坐标即可.
解:(1)对于直线y=![]() x+1,令x=0,得到y=1;令y=0,得到x=﹣2,
x+1,令x=0,得到y=1;令y=0,得到x=﹣2,
∴A(﹣2,0),B(0,1),
在Rt△AOB中,OA=2,OB=1,
根据勾股定理得:AB=![]() =
=![]() ;
;
(2)作CE⊥y轴,DF⊥x轴,可得∠CEB=∠AFD=∠AOB=90°,
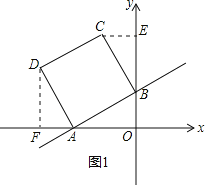
∵正方形ABCD,
∴BC=AB=AD,∠DAB=∠ABC=90°,
∴∠DAF+∠BAO=90°,∠ABO+∠CBE=90°,
∵∠DAF+∠ADF=90°,∠BAO+∠ABO=90°,
∴∠BAO=∠ADF=∠CBE,
∴△BCE≌△DAF≌ABO,
∴BE=DF=OA=2,CE=AF=OB=1,
∴OE=OB+BE=2+1=3,OF=OA+AF=2+1=3,
∴C(﹣1,3),D(﹣3,2);
(3)找出B关于x轴的对称点B′,连接B′D,与x轴交于点M,此时△BMD周长最小,
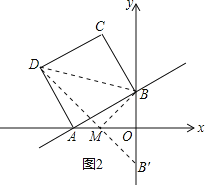
∵B(0,1),
∴B′(0,﹣1),
设直线B′D的解析式为y=kx+b,
把B′与D坐标代入得:![]() ,
,
解得:![]() ,即直线B′D的解析式为y=﹣x﹣1,
,即直线B′D的解析式为y=﹣x﹣1,
令y=0,得到x=﹣1,即M(﹣1,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案