Question

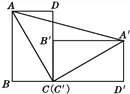
【题目】观察思考：如图， 、是直线上的两个定点，点、在直线上运动（点在点的左侧），，已知， 、间的距离为，连接、、，把沿折叠得．

（）当、两点重合时，则__________ ．

（）当、两点不重合时，

①连接，探究与的位置关系，并说明理由．

②若以、、、为顶点的四边形是矩形，画出示意图并直接写出的长．

Answer 1

【答案】（1）4；

（2）①，理由见解析；②画图见解析， 的长为或或．

【解析】试题分析：（1）当A1、D两点重合时，可以证到四边形ACDB是菱形，从而得到AC=AB=4cm；

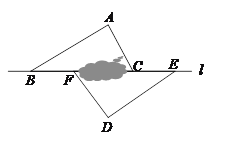
（2）①过点A1作A1E⊥BC，垂足为E，过点D作DF⊥BC，垂足为F，如图2，可以证到S△DBC=S△ABC=S△A1BC，从而得到DF=A1E，由A1E⊥BC，DF⊥BC可以证到A1E∥DF，从而得到四边形A1DFE是平行四边形，就可得到A1D∥BC；

②若以A1、C、B、D为顶点的四边形是矩形，则有三个位置，分别是图3①、图3②、图3③．对于图3①、图3②，过点C作CH⊥AB，垂足为H，运用相似三角形的性质建立方程就可求出AH，然后运用勾股定理就可求出AC的长；对于图3③，直接运用勾股定理就可求出AC的长．

试题解析：解：（1）当A1、D两点重合时，如图1①和图1②．

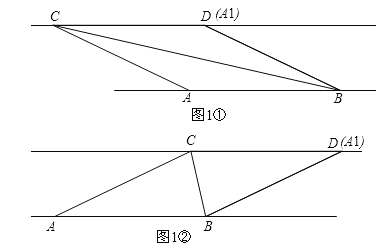
∵CD∥AB，CD=AB，∴四边形ACDB是平行四边形．

∵△ABC沿BC折叠得△A1BC，A1、D两点重合，∴AC=A1C=DC，∴平行四边形ACDB是菱形，∴AC=AB=4（cm）．故答案为：4．

（2）当A1、D两点不重合时，①A1D∥BC．

证明：过点A1作A1E⊥BC，垂足为E，过点D作DF⊥BC，垂足为F，如图2．

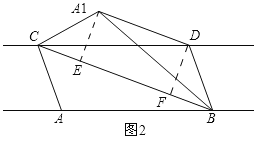
∵CD∥AB，CD=AB，∴四边形ACDB是平行四边形，∴S△ABC=S△DBC．

∵△ABC沿BC折叠得△A1BC，∴S△ABC=S△A1BC，∴S△DBC=S△A1BC，∴ BCDF=BCA1E，∴DF=A1E．

∵A1E⊥BC，DF⊥BC，∴∠A1EB=∠DFB=90°，∴A1E∥DF，∴四边形A1DFE是平行四边形，∴A1D∥EF，∴A1D∥BC．

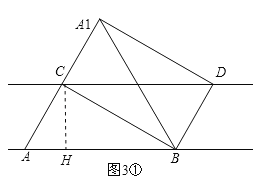
②Ⅰ．如图3①，过点C作CH⊥AB，垂足为H，此时AH＜BH．

∵四边形A1DBC是矩形，∴∠A1CB=90°．

∵△ABC沿BC折叠得△A1BC，∴∠ACB=∠A1CB，∴∠ACB=90°．

∵CH⊥AB，∴∠AHC=∠CHB=90°，∴∠ACH=90°﹣∠HCB=∠CBH，∴△AHC∽△CHB，∴ ，∴CH2=AHBH．

∵AB=4，CH=，∴3=AH（4﹣AH）．

解得：AH=1或AH=3．

∵AH＜BH，∴AH=1，∴AC2=CH2+AH2=3+1=4，∴AC=2．

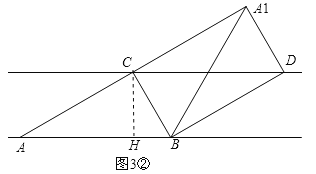
Ⅱ．如图3②，过点C作CH⊥AB，垂足为H，此时AH＞BH．

同理可得：AH=3，∴AC2=CH2+AH2=3+9=12，∴AC=．

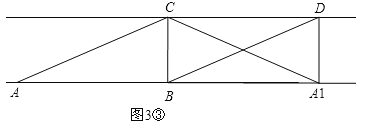
Ⅲ．如图3③，∵四边形A1DCB是矩形，∴∠A1BC=90°．∵△ABC沿BC折叠得△A1BC，∴∠ABC=∠A1BC，∴∠ABC=90°，∴AC2=BC2+AB2=3+16=19，∴AC=．

综上所述；当以A1、C、B、D为顶点的四边形是矩形时，AC的长为2或或．