Question

△ABC中，∠A，∠B，∠C的对边分别为a，b，c，下列命题中的假命题是（　　）

A．若∠A=∠C－∠B，则∠C=90º

B．若∠C=90º，则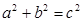

C．若∠A=30º，∠B=60º，则AB=2BC

D．若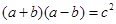，则∠C=90º

 

Answer 1

【答案】

D

【解析】

试题分析：根据直角三角形的性质和判断，勾股定理依次分析各项即可得到结论。

A．若∠A=∠C－∠B，则∠C =∠A+∠B =90º，这是一个真命题；

B．若∠C=90º，则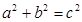，这是一个真命题；

C．若∠A=30º，∠B=60º，则∠C =90º，则AB=2BC，这是一个真命题；

D．若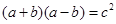，则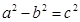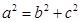，，则∠A=90º，故这是一个假命题，

故选D.

考点：本题考查的是直角三角形的性质，勾股定理

点评：解答本题的关键是掌握勾股定理，明确最大的边所对的角是直角。