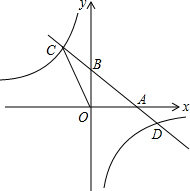
题目内容
直线y=-2x+5分别与x轴,y轴交于点C、D,与反比例函数y=
的图象交于点A、B.过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,连接EF,下列结论:①AD=BC;②EF∥AB;③四边形AEFC是平行四边形;④S△AOD=S△BOC.其中正确的个数是( )

| 3 |
| x |
| A.1 | B.2 | C.3 | D.4 |

如右图所示,
①∵y=-2x+5与y=
相交,
∴
,
解得
或
,
∴A点坐标是(1,3),B点坐标是(
,2),
∵直线y=-2x+5与x轴和y轴的交点分别是(
,0)、(0,5),
∴C点坐标是(
,0),D点坐标是(0,5),
∵AE⊥y轴,BF⊥x轴,
∴AE=1,DE=OD-OE=5-3=2,
在Rt△ADE中,AD=
=
,
同理可求BC=
,
故AD=BC,
故①选项正确;
②∵OF:OE=1:2,OC:OD=1:2,
∴EF∥AB,
故②选项正确;
③∵AE=CF=1,且AE∥CF,
∴四边形AEFC是平行四边形,
故③选项正确;
④∵S△AOD=
•OD•AE=
×5×1=2.5,
S△BOC=
•OC•BF=
×
×2=2.5,
∴S△AOD=S△BOC,
故④选项正确.
故选D.

①∵y=-2x+5与y=
| 3 |
| x |
∴
|
解得
|
|
∴A点坐标是(1,3),B点坐标是(
| 3 |
| 2 |
∵直线y=-2x+5与x轴和y轴的交点分别是(
| 5 |
| 2 |
∴C点坐标是(
| 5 |
| 2 |
∵AE⊥y轴,BF⊥x轴,
∴AE=1,DE=OD-OE=5-3=2,
在Rt△ADE中,AD=
| 12+22 |
| 5 |
同理可求BC=
| 5 |
故AD=BC,
故①选项正确;
②∵OF:OE=1:2,OC:OD=1:2,
∴EF∥AB,
故②选项正确;
③∵AE=CF=1,且AE∥CF,
∴四边形AEFC是平行四边形,
故③选项正确;
④∵S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴S△AOD=S△BOC,
故④选项正确.
故选D.


练习册系列答案
相关题目
 ,一次函数图象与y轴的交点为C.
,一次函数图象与y轴的交点为C.


 A=3,点C的横坐标为-3,tan∠BAO=
A=3,点C的横坐标为-3,tan∠BAO= 过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.
过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.



 D两点.
D两点.