题目内容
如图①,AB是半圆O的直径,以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D,其中OA=4.
(1)判断线段AP与PD的大小关系,并说明理由;
(2)连接OD,当OD与半圆C相切时,求 的长;
的长;
(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.
解:(1)AP=PD。理由如下:
如图①,连接OP,OD,
∵OA是半圆C的直径,∴∠APO=90°,即OP⊥AD。
又∵OA=OD,∴AP=PD。
(2)如图①,连接PC、OD.
∵OD是半圆C的切线,∴∠AOD=90°。
由(1)知,AP=PD.
又∵AC=OC,∴PC∥OD。∴∠ACP=∠AOD=90°。
∵OA=4,∴AC=2。
∴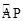 的长=
的长=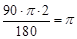 。
。
(3)分两种情况:
①当点E落在OA上(即0<x≤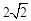 时),如图②,
时),如图②,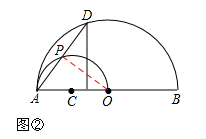
连接OP,则∠APO=∠AED.
又∵∠A=∠A,∴△APO∽△AED。∴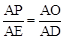 。
。
∵AP=x,AO=4,AD=2x,AE=4﹣y,∴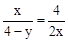 。
。
∴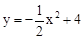 (0<x≤
(0<x≤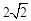 ).
).
②当点E落在线段OB上(即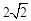 <x<4)时,如图③,
<x<4)时,如图③,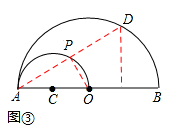
连接OP,同①可得,△APO∽△AED。
∴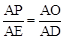 。
。
∵AP=x,AO=4,AD=2x,AE=4+y,∴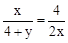 。
。
∴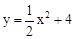 (
(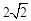 <x<4)。
<x<4)。
综上所述,y与x之间的函数关系式为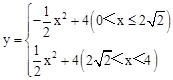
解析试题分析:(1)AP=PD.理由如下:如图①,连接OP.利用圆周角定理知OP⊥AD.然后由等腰三角形“三合一”的性质证得AP=PD。
(2)由三角形中位线的定义证得CP是△AOD的中位线,则PC∥DO,所以根据平行线的性质、切线的性质易求弧AP所对的圆心角∠ACP=90°,从而求出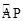 的长。
的长。
(3)分类讨论:点E落在线段OA和线段OB上,这两种情况下的y与x的关系式.这两种情况都是根据相似三角形(△APO∽△AED)的对应边成比例来求y与x之间的函数关系式。

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )
A.y= | B.y= | C.y= | D.y= |
 经过A、C两点,与x轴的另一个交点是点D,连接BD.
经过A、C两点,与x轴的另一个交点是点D,连接BD.


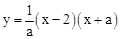 (a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.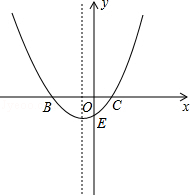

 时,y的值.
时,y的值.