题目内容
如图,抛物线y=a(x﹣h)2+k经过点A(0,1),且顶点坐标为B(1,2),它的对称轴与x轴交于点C.
(1)求此抛物线的解析式.
(2)在第一象限内的抛物线上求点P,使得△ACP是以AC为底的等腰三角形,请求出此时点P的坐标.
(3)上述点是否是第一象限内此抛物线上与AC距离最远的点?若是,请说明理由;若不是,请求出第一象限内此抛物线上与AC距离最远的点的坐标.
解:(1)∵抛物线y=a(x﹣h)2+k顶点坐标为B(1,2),
∴y=a(x﹣1)2+2。
∵抛物线经过点A(0,1),∴a(0﹣1)2+2=1,解得a=﹣1。
∴此抛物线的解析式为y=﹣(x﹣1)2+2,即y=﹣x2+2x+1。
(2)∵A(0,1),C(1,0),∴OA=OC。
∴△OAC是等腰直角三角形。
过点O作AC的垂线l,根据等腰三角形的“三线合一”的性质知:l是AC的中垂线,
∴l与抛物线的交点即为点P。
如图,直线l的解析式为y=x,
解方程组 ,
,
得 或
或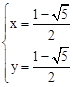 (不合题意舍去)。
(不合题意舍去)。
∴点P的坐标为(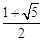 ,
,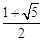 )。
)。
(3)点P不是第一象限内此抛物线上与AC距离最远的点.
由(1)知,点C的坐标为(1,0),
设直线AC的解析式为y=kx+b,
则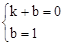 ,解得
,解得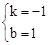 。
。
∴直线AC的解析式为y=﹣x+1.
设与AC平行的直线的解析式为y=﹣x+m.
解方程组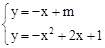 ,代入消元,得﹣x2+2x+1=﹣x+m,即x2﹣3x+m﹣1=0。
,代入消元,得﹣x2+2x+1=﹣x+m,即x2﹣3x+m﹣1=0。
∵此点与AC距离最远,∴直线y=﹣x+m与抛物线有且只有一个交点。
∴方程x2﹣3x+m﹣1=0有两个相等的实数根。
△=9﹣4(m﹣1)=0,解之得m=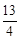 。
。
∴x2﹣3x+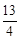 ﹣1=0,解得x1=x2=
﹣1=0,解得x1=x2=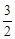 ,此时y=
,此时y= 。
。
∴第一象限内此抛物线上与AC距离最远的点的坐标为(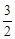 ,
, )。
)。
解析试题分析:(1)由抛物线y=a(x﹣h)2+k的顶点坐标是B(1,2)知:h=1,k=2,则y=a(x﹣1)2+2,再把A点坐标代入此解析式即可。
(2)易知△OAC是等腰直角三角形,可得AC的垂直平分线是直线y=x,根据“线段垂直平分线上的点到线段两个端点的距离相等”知直线y=x与抛物线的交点即为点P,解方程组即可求出P点坐标。
(3)先求出第一象限内此抛物线上与AC距离最远的点的坐标,再与P点的坐标比较进行判断.满足条件的点一定是与直线AC平行且与抛物线有唯一交点的直线与抛物线相交产生的,易求出直线AC的解析式,设出与AC平行的直线的解析式,令它与抛物线的解析式组成的方程组有唯一解,求出交点坐标,通过判断它与点P是否重合来判断点P是否是第一象限内此抛物线上与AC距离最远的点。

 的抛物线
的抛物线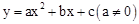 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
 ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。 ,求点P的坐标;
,求点P的坐标;

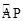 的长;
的长;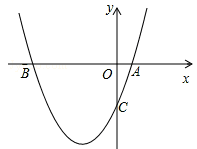
 ).
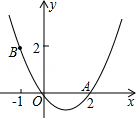
). (a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
 (k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )