Question

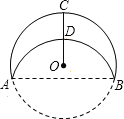
【题目】如图，将半径为8的⊙O折叠，弧AB恰好经过与AB垂直的半径OC的中点D，则折痕AB的长___________ .

Answer 1

【答案】

【解析】

延长CO交AB于E点，交⊙O于点F，连接OB，由OC与AB垂直，根据垂径定理得到E为AB的中点，然后利用D是OC的中点和对称即可求出OD、CD、DE的长，从而求出OE，然后由OB，OE的长，根据勾股定理求出AE的长，进而得出AB的长．

解：延长CO交AB于E点，交⊙O于点F，连接OB，

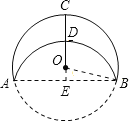
∵CE⊥AB，

∴E为AB的中点，

∵D是OC的中点，OC=8

∴CD=4，OD=4，OB=8，CF=2OC=16

根据对称的性质可得：

DE=DF=（CF－CD）=6

OE=DE－OD=2

在Rt△OEB中，根据勾股定理可得：

∴AB=

故答案为.