��Ŀ����
����Ŀ��ij���ϳ���300ǧ�˵�A�ֹ�֭��240ǧ�˵�B�ֹ�֭Ϊԭ�ϣ����������ס��������������ϣ���֪ÿǧ�˼������Ϻ�0.6ǧ��A�ֹ�֭����0.3ǧ��B�ֹ�֭��ÿǧ���������Ϻ�0.2ǧ��A�ֹ�֭����0.4ǧ��B�ֹ�֭�����ϳ��ƻ������ס��������������Ϲ�650ǧ�ˣ���ó�������������x��ǧ�ˣ���
��1���г���������Ĺ���x�IJ���ʽ�飬�����x��ȡֵ��Χ��
��2����֪�����ϳ��ļ����������ۼ���ÿ1ǧ��3Ԫ�������������ۼ���ÿ1ǧ��4Ԫ����ô�����ϳ������ס����������ϸ�����ǧ�ˣ�����ʹ���������������ܽ�����
���𰸡��⣺��1����ó�������������xǧ�ˣ��������������ϣ�650��x��ǧ�ˣ�
��������ã�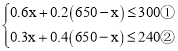 ��
��
�����ã�x��425�������ã�x��200��
��x��ȡֵ��Χ��200��x��425��
��2�����������������ܽ��ΪyԪ����������ã�
![]() ����y=��x+2600��
����y=��x+2600��
��k=��1��0��
����x=200ʱ���������������ܽ�����Ϊ��200+2600=2400Ԫ��
��������
�����������1����ʾ�������������ϣ�650��x��ǧ�ˣ�Ȼ���������A�ֹ�֭��B�ֹ�֭�������г�һԪһ�β���ʽ�飬��⼴�ɵõ�x��ȡֵ��Χ��
��2�����������ܽ������������ϵ����۶�ĺ���ʽ�������ٸ���һ�κ��������������������۶

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�



