题目内容
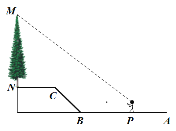
【题目】如图，
是垂直于水平面的一棵树，小马（身高1.70米）从点
出发，先沿水平方向向左走10米到
点，再经过一段坡度
，坡长为5米的斜坡
到达
点，然后再沿水平方向向左行走5米到达
点（、、、在同一平面内），小马在线段
的黄金分割点
处（
）测得大树的顶端
的仰角为37°，则大树的高度约为（ ）米.（参考数据：
）
A. 7.8米 B. 8.0米 C. 8.1米 D. 8.3米
【答案】D
【解析】
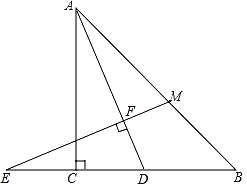
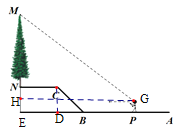
作GH⊥MN于H，CD⊥AB于D．想办法求出GH、MH即可解决问题；
解：作GH⊥MN于H，CD⊥AB于D．则四边形CDEN,EHPG是矩形．
在Rt△BCD中，CD：BD=3：4，BC=5m，
∴CD=NE=3m，BD=4m，NC=ED=5m，
∴
在Rt△MHG中，MH=GHtan37°≈10.635m，
∵NH=NE-HE=4-2.3=1.7m，
∴MN=MH﹣NH=10.635-2.3≈8.3（m），
故选：D．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
