题目内容
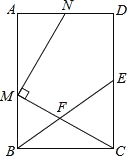
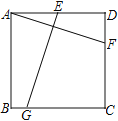
【题目】如图，在边长为6的正方形ABCD中，点F为CD上一点，E是AD的中点，且DF＝2．在BC上找点G，使EG＝AF，则BG的长是___________
【答案】1或5
【解析】
过E作EH⊥BC于H，取
，根据平行线分线段成比例定理得：BH=CH=3，证明Rt△ADF≌Rt△EHG，得GH=DF=2，可得BG的长，再运用等腰三角形的性质可得BG及
的长．
解：如图：过E作EH⊥BC于H，取 ,则AB∥EH∥CD，
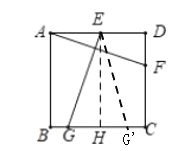
∵E是AD的中点，
∴BH=CH=3，
∵四边形ABCD是正方形，
∴AD=CD=EH，∠D=∠EHG=90°，
∵EG=AF，
∴Rt△ADF≌Rt△EHG(HL)，
∴GH=DF=2，
∴BG=BHGH=32=1；
∵
∴
∴
故答案为：1或5．
练习册系列答案
名校课堂系列答案
相关题目
