题目内容
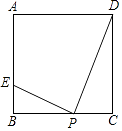
【题目】如图，在△ABC中，∠BAC=90°，AD是中线，E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．试判断四边形ADCF的形状，并证明你的结论．
【答案】四边形ADCF是菱形，证明见解析
【解析】试题分析：根据AAS证△AFE≌△DBE，利用全等三角形的对应边相等得到AF=BD．结合已知条件，利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形，由“直角三角形斜边的中线等于斜边的一半”得到AD=DC，从而得出结论．
试题解析：解：四边形ADCF是菱形．理由如下：
∵AF∥BC，∴∠AFE=∠DBE．∵E是AD的中点，AD是BC边上的中线，∴AE=DE，BD=CD．在△AFE和△DBE中，∵∠AFE=∠DBE，∠FEA=∠BED，AE=DE，∴△AFE≌△DBE（AAS），∴AF=DB．∵DB=DC，∴AF=CD．∵AF∥BC，∴四边形ADCF是平行四边形．∵∠BAC=90°，D是BC的中点，∴AD=DC=
BC，∴四边形ADCF是菱形．
练习册系列答案
相关题目
