��Ŀ����
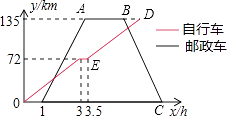
����Ŀ��Ϊ������̼�����ɫ���У�ij���г����ֲ�������ĩ��֯��Զ�����С�������г��ӴӼس�����;���ҵض�����Ϣ��ɲ�������������Ŀ�ĵر��أ����г��ӳ���1Сʱ��ǡ��һ���������Ӽس����������г����н�·��ǰ�����أ��ڱ������2Сʱװж������ԭ·���ؼأ����г�������������ʻ�ٶȾ����ֲ��䣬������������ʻ�ٶ������г�����ʻ�ٶȵ�2.5������ͼ��ʾ���г��ӡ���������ص�·��y��km�������г����뿪��ʱ��x��h���ĺ�����ϵͼ�������ͼ���ṩ����Ϣ������и��⣺ 
��1�����г�����ʻ���ٶ���km/h��
��2����������������Сʱ�����г����״�������
��3���������ڷ���;�������г����ٴ�����ʱ�ĵص����ض�Զ��
���𰸡�
��1��24
��2���⣺�������
���������ٶ�Ϊ��24��2.5=60km/h��
������������aСʱ�����������������
24��a+1��=60a��
��ã�a= ![]() ��
��
������������ ![]() Сʱ�����г����״�����
Сʱ�����г����״�����
��3���⣺�����⣬��
������������ص�ʱ��Ϊ��135��60= ![]() ��
��
���������ӱ��س�����ʱ��Ϊ�� ![]() ��
��
��B�� ![]() ��135����C��7.5��0����
��135����C��7.5��0����
���г��ӵ�����ص�ʱ��Ϊ��135��24+0.5= ![]() +0.5=
+0.5= ![]() ��
��
��D�� ![]() ��135����
��135����
��BC�Ľ���ʽΪy1=k1x+b1���������
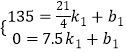 ��
��
�� ![]() ��
��
��y1=��60x+450��
��ED�Ľ���ʽΪy2=k2x+b2���������
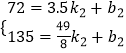 ��
��
��ã� ![]() ��
��
��y2=24x��12��
��y1=y2ʱ��
��60x+450=24x��12��
��ã�x=5.5��
y1=��60��5.5+450=120��
���������ڷ���;�������г����ٴ�����ʱ�ĵص�����120km��
���������⣺��1������������г�����ʻ���ٶ��ǣ�72��3=24km/h�����Դ��ǣ�24����1�����ٶ�=·�̡�ʱ��Ϳ���������ۣ���2�������г����ٶȾͿ���������������ٶȣ�����������������������aСʱ���������������������⼴�ɣ���3�������������ٶȿ������B�������C�����꣬�����г����ٶȾͿ���D�����꣬�ɴ���ϵ�����Ϳ������BC��ED�Ľ���ʽ�Ϳ���������ۣ�