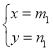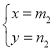题目内容
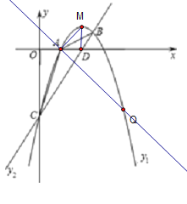
【题目】如图,已知抛物线y1=ax+bx+c的顶点坐标为M(2,1),且经过点B![]() ,抛物线对称轴左侧与
,抛物线对称轴左侧与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点C.
轴交于点C.

(1)求抛物线解析式y1和直线BC的解析式y2;
(2)连接AB、AC,求△ABC的面积.
(3)根据图象直接写出y1<y2时自变量![]() 的取值范围.
的取值范围.
(4)若点Q是抛物线上一点,且QA⊥MA,求点Q的坐标.
【答案】(1)y1=x2+4x3,![]() ;(2)
;(2)![]() ;(3)x<0或x>
;(3)x<0或x>![]() ;(4)Q(4,-3).
;(4)Q(4,-3).
【解析】
(1)设抛物线顶点式解析式y1=a(x-2)2+1,然后把点B的坐标代入求出a的值,即可求出抛物线解析式;令x=0求出点C的坐标,再设直线BC的解析式y2=kx+b(k≠0),利用待定系数法求一次函数解析式;
(2)令y=0,利用抛物线解析式求出点A的坐标,设直线BC与x轴的交点为D,利用直线BC的解析式求出点D的坐标,然后根据S△ABC=S△ABD+S△ACD,列式进行计算即可得解;
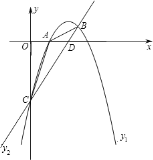
(3)根据图形,找出直线BC在抛物线上方部分的x的取值范围即可;
(4)连接MD,AM,过点A作AQ⊥AM,易得∠MAD=45°,即∠QAD=45°,从而得出Q点横纵坐标之间的关系,代入抛物线解析式求出Q点的坐标.
(1)∵抛物线的顶点坐标为(2,1),
∴y1=a(x2)2+1,
∵抛物线经过点![]() ,
,
∴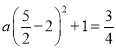 ,
,
解得a=1,
∴y1=(x2)2+1=x2+4x3,
当x=0,y=3,
∴C(0,3),
设直线BC解析式为y2=kx+b(k≠0),
则有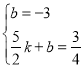 ,
,
解得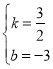
所以,直线BC的解析式为![]() ;
;
(2)对于y1=x2+4x3,当y=0时,x2+4x3=0,
即x24x+3=0,
解得x1=1,x2=3,
∴点A的坐标为(1,0),
设直线BC与x轴相交于D,
对于![]() ,当y=0时,
,当y=0时, ![]() ,
,
解得x=2,
∴点D的坐标为(2,0),
∴AD=21=1,
则S△ABC=S△ABD+S△ACD,
=![]()
=![]()
=![]() .
.
(3)由图得,当x<0或x>![]() 时,y1<y2.
时,y1<y2.
(4)连接MD,AM,过点A作AQ⊥AM.
∵M(2,1),D(2,0)
∴MD ⊥ x轴
∵A(1,0)
∴AD=MD,即△ADM为等腰直角三角形,
∴∠MAD=45°,即∠QAD=45°,
∴设Q(m,1-m)
则![]() ,解得m1=1(舍去),m2=4,
,解得m1=1(舍去),m2=4,
∴Q(4,-3).