Question

【题目】如图，线段 AB 的长为 4，C 为 AB 上一个动点，分别以 AC、BC 为斜边在 AB 的同侧作两个等腰直角三角形 ACD 和 BCE， 连结 DE， 则 DE 长的最小值是( )

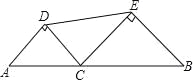
A. B. 2C. D. 4

Answer 1

【答案】B

【解析】

设AC=x，BC=4-x，根据等腰直角三角形性质，得出CD=x，CE=（4-x），根据勾股定理然后用配方法即可求解．

解：设 AC=x，BC=4﹣x，

∵△CDA，△BCE 均为等腰直角三角形，

∴CD=x，CE=(4﹣x)，

∵∠ACD=45°，∠BCE=45°，

∴∠DCE=90°，

∴DE=CD+CE=

∵根据二次函数的最值，

∴当 x 取 2 时 ，DE取最小值 ，最小值为：2．

故答案为：B.