题目内容
 如图,已知点A(-2,4)和点B(1,0)都在抛物线y=mx2+2mx+n上.
如图,已知点A(-2,4)和点B(1,0)都在抛物线y=mx2+2mx+n上.(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形AA′B′B为菱形,求平移后抛物线的表达式;
(3)试求出菱形AA′B′B的对称中心点M的坐标.
分析:(1)本题需先根据题意把A (-2,4)和点B (1,0)代入抛物线y=mx2+2mx+n中,解出m、n的值即可.
(2)本题需先根据四边形AA′B′B为菱形得出y的解析式,再把解析式向右平移5个单位即可得到平移后抛物线的表达式.
(3)本题需根据平移与菱形的性质,得到A′、B′的坐标,再过点A′作A′H⊥x轴,得出BH和A′H的值,再设菱形AA′B′B的中心点M,作MG⊥x轴,根据中位线性质得到MG、BG的值,最后求出点M的坐标.
(2)本题需先根据四边形AA′B′B为菱形得出y的解析式,再把解析式向右平移5个单位即可得到平移后抛物线的表达式.
(3)本题需根据平移与菱形的性质,得到A′、B′的坐标,再过点A′作A′H⊥x轴,得出BH和A′H的值,再设菱形AA′B′B的中心点M,作MG⊥x轴,根据中位线性质得到MG、BG的值,最后求出点M的坐标.
解答:解:(1)根据题意,把A (-2,4)和点B (1,0)代入抛物线y=mx2+2mx+n中,
解得
;
(2)四边形AA′B′B为菱形,
则AA′=B′B=AB=5;
∵y=-
x2-
x+4,
=-
(x+1)2+
;
∴向右平移5个单位的抛物线解析式为,
y=-
(x-4)2+
;
(3)根据平移与菱形的性质,得到
A′(3,4),B′(6,0);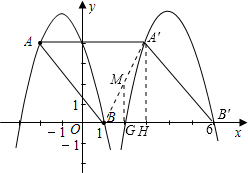
过点A′作A′H⊥x轴,
在Rt△A′BH中,点H(3,0),点B(1,0),
故BH=2,A′H=4;
设菱形AA′B′B的中心点M,作MG⊥x轴,
根据中位线性质得
MG=
A′H=2,
BG=
BH=1;
因此菱形AA′B′B的中心点M坐标为(2,2).
解得
|
(2)四边形AA′B′B为菱形,
则AA′=B′B=AB=5;
∵y=-
| 4 |
| 3 |
| 8 |
| 3 |
=-
| 4 |
| 3 |
| 16 |
| 3 |
∴向右平移5个单位的抛物线解析式为,
y=-
| 4 |
| 3 |
| 16 |
| 3 |
(3)根据平移与菱形的性质,得到
A′(3,4),B′(6,0);

过点A′作A′H⊥x轴,
在Rt△A′BH中,点H(3,0),点B(1,0),
故BH=2,A′H=4;
设菱形AA′B′B的中心点M,作MG⊥x轴,
根据中位线性质得
MG=
| 1 |
| 2 |
BG=
| 1 |
| 2 |
因此菱形AA′B′B的中心点M坐标为(2,2).
点评:本题主要考查了二次函数的应用问题,在解题时要根据二次函数的图象和性质进行综合分析是本题的关键.

练习册系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )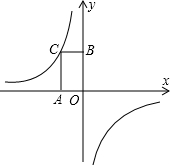 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=