题目内容
如图:四边形ABCD和四边形AEFC都是矩形,点B在EF边上.
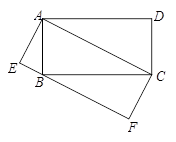
(1)请你找出图中一对相似三角形(相似比不等于1),并加以证明;
(2)若四边形ABCD的面积为20,求四边形AEFC的面积.

(1)请你找出图中一对相似三角形(相似比不等于1),并加以证明;
(2)若四边形ABCD的面积为20,求四边形AEFC的面积.
(1)证明见解析;(2)20.
试题分析:(1)由于四边形ABCD和四边形AEFC都是矩形,易在图形中找到两三角形相似,如:△AEB ∽△CBA或△AEB∽△BFC;△AEB∽△ADC;△CAB∽△BFC;△BFC∽△ADC .
(2)因为
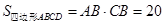 ,又△AEB∽△CBA,所以
,又△AEB∽△CBA,所以 ,即
,即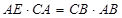 ,从而可求出四边形AEFC的面积.
,从而可求出四边形AEFC的面积.试题解析:(1)△AEB∽△CBA.(或△AEB∽△BFC;△AEB∽△ADC;△CAB∽△BFC;△BFC∽△ADC.)
证明:∵四边形ABCD和四边形AEFC是矩形,
∴∠E=∠CBA=∠EAC=90°.
∵∠EAB+∠CAB=90°,∠EAB+∠ABE=90°,
∴∠ABE=∠CAB.
∴△AEB∽△CBA.
(2)∵△AEB∽△CBA,
∴
 .
.∴
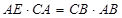 .
.∵

∴
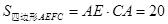
考点: 相似三角形的判定与性质.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 .求证:DE∥BC
.求证:DE∥BC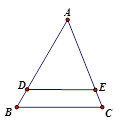
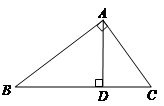
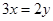 ,那么
,那么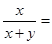 .
.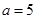 ,
,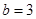 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.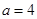 ,
,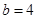 时,
时,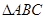 为圆O的内接三角形,
为圆O的内接三角形,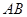 为直径,过C作
为直径,过C作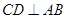 于D,设
于D,设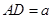 ,BD=b.
,BD=b.
 表示线段OC,CD;
表示线段OC,CD;
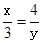
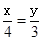
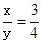
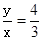
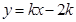 的图像与两坐标轴围成的三角形面积是( )
的图像与两坐标轴围成的三角形面积是( )