题目内容
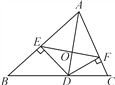
【题目】如图，在△ABC中，CE⊥AB于点E，DF⊥AB于点F，CE平分∠ACB，DF平分∠BDE，
求证：AC∥ED.
证明：∵CE⊥AB于E，DF⊥AB于F（已知）
∴DF∥ （垂直于同一条直线的两直线平行）
∴∠BDF=∠ （ ）
∠FDE=∠ （两直线平行，内错角相等）
∵CE平分∠ACB，DF平分∠BDE（已知）
∴∠ACE=∠ECB，∠EDF=∠BDF（角平分线的定义）
∴∠ACE=∠ （等量代换）
∴AC∥ED（ ）.
【答案】CE；BCE；两直线平行，同位角相等；DEC；DEC；内错角相等，两直线平行.
【解析】根据垂直证明DF∥CE，利用平行线的性质和角平分线的定义得出∠ACE=∠DEC，进而利用平行线判定解答即可．
详证明：∵CE⊥AB于E，DF⊥AB于F（已知）
∴DF∥CE（垂直于同一条直线的两直线平行）
∴∠BDF=∠BCE（两直线平行，同位角相等）
∠FDE=∠DEC（两直线平行，内错角相等）
∵CE平分∠ACB，DF平分∠BDE（已知）
∴∠ACE=∠ECB，∠EDF=∠BDF（角平分线的定义）
∴∠ACE=∠DEC（等量代换）
∴AC∥ED（内错角相等，两直线平行）．
故答案为：CE；BCE；两直线平行，同位角相等；DEC；DEC；内错角相等，两直线平行．
练习册系列答案
阅读快车系列答案
相关题目
