题目内容
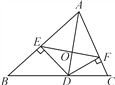
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是_________.(填序号)
【答案】②③④
【解析】试题解析:根据已知条件不能推出OA=OD,∴①错误;
∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,
![]() ,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AD平分∠BAC,
∴AD⊥EF,∴②正确;
∵∠BAC=90°,∠AED=∠AFD=90°,
∴四边形AEDF是矩形,
∵AE=AF,
∴四边形AEDF是正方形,∴③正确;
∵AE=AF,DE=DF,
∴AE2+DF2=AF2+DE2,∴④正确;
∴②③④正确,

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目





