题目内容
【题目】如图,在平面直角坐标系xOy中,A(a,0),B(0,b),C(-a,0),且![]() +b2-4b+4=0.
+b2-4b+4=0.
(1)求证:∠ABC=90°;
(2)∠ABO的平分线交x轴于点D,求D点的坐标.
(3)如图,在线段AB上有两动点M、N满足∠MON=45°,求证:BM2+AN2=MN2.


【答案】(1)证明见解析(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)根据非负数的性质求出a、b的值,根据直角三角形的判定定理证明;
(2)过D作DE⊥AB于E,由于BD是∠ABO的角平分线,根据角平分线的性质知DO=DE,即可证得OD=DE,根据三角形的面积公式计算即可;
(3)把△OBM绕点O顺时针旋转90°,则旋转后B点与A点重合,点M对应点E,连结NE,由于∠MON=45°,那么∠EON=∠MON=45°,即可证得△MON≌△EON,MN=NE;同理可通过证△MON≌△EON,来得到BM=AN,∠OAE=∠OBM=45°,因此在Rt△NAE中,根据勾股定理即可证明.
(1)证明:由![]() 得
得
![]() ,
,
∴![]()
∴![]()
∴A、B、C的坐标是A(2,0),B(0,2),C(-2,0)
∴AB=![]() ,BC=
,BC=![]() ,AC=4
,AC=4
∴AC2=AB2+BC2
∴∠ABC=90°
(2)过点D作DE⊥AB于E,
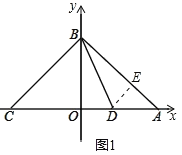
∵BD平分∠ABO,
∴OD=DE,
设OD=x,
∵![]() 解得,
解得,![]() ,
,
∴D点的坐标是![]()
(3)证明:把△OBM绕点O顺时针旋转90°,则旋转后B点与A点重合,点M对应点E(如图),连结NE
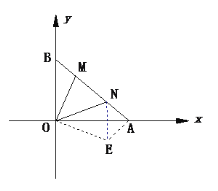
∴∠NAE=90°
又∠MON=45°,
∴∠NOE=45°
在△MON和△EON中,

∴△OMN≌△OEN(SAS)
∴MN=NE
在△MOB和△EOA中,
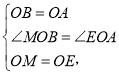
∴△MOB≌△EOA,
BM=AE
∴在Rt△NAE中
NE2=AN2+AE2
∴MN2=AN2+BM2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目