题目内容
【题目】已知四边形
的对角线
，
，
、
、
、
分别是
、
、
、
的中点，则
的值是_______．
【答案】118
【解析】
先根据
、
、
、
分别是
、
、
、
的中点得到四边形PQRS是平行四边形，再根据平行四边形的对角线的平方与四条边边长的平方的关系即可得到答案．
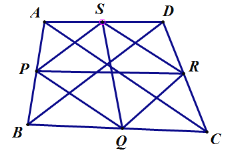
∵、、、分别是、、、的中点，
∴
=
（中位线的性质），
同理可得:
=
并且有 PS∥BD，PS=BD（中位线的性质），
同理可得：QR∥BD，QR=
，
∴PS∥QR，
（等量替换），
∴四边形PQRS是平行四边形，
∴
=
+
（平行四边形两条对角线的平方和等于四条边长的平方和，后附证明过程）
= 
=27+32+27+32
=118．
附：四边形ABCD是平行四边形，则
=
+
证明： 如图，作
垂直于E，作
垂直于的延长线，交于点F.
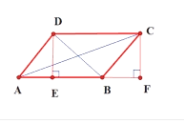
∵四边形ABCD是平行四边形，
∴AB∥DC，AB=DC，AD=BC，
∴DE=CF（两平行线间的距离相等），
∴Rt△AED≌Rt△BFC（HL）
∴AE=BF，
根据勾股定理得：
,
,
,
=
=
∵
（勾股定理）
∴=+（等量替换）．
练习册系列答案
相关题目
